web-dev-qa-db-fra.com

Quel est l'algorithme de tri le plus obscur que vous connaissez?

Je viens de lire à propos de Cyclesort via un poteau de blog Sortvis.org. C'est probablement le plus obscur que j'ai entendu parler jusqu'à présent, car il utilise des mathématiques que je ne connais pas (détecter les cycles de permutations d'ensembles entiers).

Quelle est la plus obscure que vous connaissez?

algorithmssorting
22
sova

Jamais entendu parler de Tri de patience ? Eh bien maintenant vous avez ...

9
Mason Wheeler

( slowsort fonctionne par multiplier et se rendre (par opposition à la division et à la conquérir). C'est intéressant car il est pratiquement l'algorithme de tri le moins efficace qui peut être construit (asymptotiquement et avec la restriction qu'un tel algorithme, tout en étant lent, doit encore tout le temps fonctionner à un résultat).

Cela la compense de BogoSort car dans le meilleur cas, BogoSort est assez efficace - à savoir lorsque le tableau est déjà trié. Slowsort n'a pas "souffert" d'un tel comportement de ce meilleur cas. Même dans son meilleur cas, il a toujours du temps d'exécution 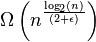$\Omega(n^\frac{\log_2n}{2+\epsilon})$ pour ε > 0.

Voici son pseudocode, adapté de l'article allemand Wikipedia :

function slowsort(A, i, j):
  if i >= j: return

  m = (i + j) / 2
  slowsort(A, i, m)
  slowsort(A, m + 1, j)

  if A[j] < A[m]:
    swap(A[j], A[m])

  slowsort(A, i, j - 1)
12
Konrad Rudolph

Sleeend Tri est plutôt roman.

    #!/bin/bash
    function f() {
        sleep "$1"
        echo "$1"
    }
    while [ -n "$1" ]
    do
        f "$1" &
        shift
    done
    wait

exemple d'utilisation:

    ./sleepsort.bash 5 3 6 3 6 3 1 4 7
6
Mike Weller

Un autre "algorithme" obscur est Tri de design intelligent - mais aucun algorithme n'est plus rapide ou a moins de consommation de mémoire :)

6
Caspar

Je pense que le tri des bulles serait la mauvaise réponse dans cette situation aussi

:)

5
OscarRyz

Knuth Volume 31, dans la réponse à l'un des exercices, donne une mise en œuvre d'un algorithme de tri sans nom qui est fondamentalement un golf de code ancien - le tri le plus court que vous pouvez écrire dans la langue de montage de mixage. Le code court vient au prix SO-mineur de O (n3) complexité bien que ...

1Au moins dans les éditions les plus anciennes. Compte tenu des modifications de Mixal pour la nouvelle édition, je ne suis pas sûr de savoir s'il est toujours là, voire de rendre le peu de sens de la minuscule dans le mixal d'origine.

3
Jerry Coffin

Pour ma classe de structures de données, j'ai dû (explicitement) prouver l'exactitude de Sooge Trier . Il a une durée de fonctionnement de O (n ^ {journal 3/log 1,5}) = O (n ^ 2.7095 ...).

3
Alex ten Brink

Je ne sais pas si c'est le plus obscur, mais Spaghetti Tri est l'une des meilleures dans les situations où vous pouvez l'utiliser.

2
Caleb

L'un des livres originaux de Knuth, le tri et la recherche de la recherche d'origine, avait un rabat moyen qui a diagrillé un processus qui trié un fichier de bande n'utilisant aucun disque dur. Je pense qu'il a utilisé six lecteurs de bande et montrait explicitement lorsque chacun était en train de lire en avant, de lire en arrière, de rembobinage ou de veille. Aujourd'hui, c'est un monument à une technologie obsolète.

2
Andy Canfield

Google Code Jam a eu un problème d'un algorithme appelé Gorosort, que je pense qu'ils ont inventé pour le problème.

Goro a 4 bras. Goro est très fort. Vous ne plaisantez pas avec Goro. Goro doit trier un tableau de n entiers différents. Les algorithmes ne sont pas la force de Goro; La force est la force de Goro. Le plan de Goro est d'utiliser les doigts sur deux de ses mains pour maintenir plusieurs éléments du tableau et frapper la table avec ses troisième et quatrième poings aussi actifs que possible. Cela fera que les éléments non garantis du tableau volent dans les airs, se mélangent aléatoirement et retombent dans les emplacements de la matrice vide.

http://code.google.com/codejam/contest/dashboard?c=975485#s=P

1
MatrixFrog

Ne me souviens pas du nom, mais c'était essentiellement

while Array not sorted

  rearrange the array in a random order
0
Akash

tri de coquille

L'algorithme lui-même n'est peut-être pas cet obscur, mais qui peut nommer une mise en œuvre réellement utilisée dans la pratique? Je peux!

TIGCC (un compilateur à base de GCC pour les calculatrices graphiques TI-89/92/V200) utilise le tri de la coque pour la mise en œuvre qsort dans sa norme une bibliothèque:

__ATTR_LIB_C__ void qsort(void *list, short num_items, short size, compare_t cmp_func)
{
  unsigned short gap,byte_gap,i,j;                
  char *p,*a,*b,temp;                       
  for (gap=((unsigned short)num_items)>>1; gap>0; gap>>=1)    // Yes, this is not a quicksort,
    {                                                         // but works fast enough...    
      byte_gap=gap*(unsigned short)size;
      for(i=byte_gap; i<((unsigned short)num_items)*(unsigned short)size; i+=size)
        for(p=(char*)list+i-byte_gap; p>=(char*)list; p-= byte_gap)
          {
            a=p; b=p+byte_gap;
            if(cmp_func(a,b)<=0) break;
            for(j=size;j;j--)
              temp=*a, *a++=*b, *b++=temp;
          }
    }
}

La tri de la coque a été choisie en faveur de QuickSort pour garder la taille du code bas. Bien que sa complexité asymptotique soit pire, le TI-89 n'a pas beaucoup de RAM (190k, moins la taille du programme et la taille totale de toutes les variables non arrêtées), il est donc quelque peu Sûr supposer que le nombre d'articles sera faible.

Une mise en œuvre plus rapide a été écrite après que je me suis plaint d'être trop lent dans un programme que j'écris. Il utilise de meilleures tailles d'écart, ainsi que des optimisations d'assemblage. On peut le trouver ici: qsort.c

0
Joey Adams