Défi de performance C ++: conversion d'entier en std :: string
Quelqu'un peut-il battre les performances de mon entier au code std :: string, lié ci-dessous?
Il y a déjà plusieurs questions qui expliquent comment convertir un entier en std::string en C++, comme celui-ci , mais aucune des solutions proposées n'est efficace.
Voici du code prêt à être compilé pour certaines méthodes courantes pour concurrencer:
- La "façon C++", en utilisant stringstream: http://ideone.com/jh3Sa
- sprintf, que les SO-ers recommandent généralement aux amateurs de performances: http://ideone.com/82kwR
Contrairement à croyance populaire , boost::lexical_cast a sa propre implémentation ( livre blanc ) et n'utilise pas stringstream et les opérateurs d'insertion numérique. J'aimerais vraiment voir ses performances comparées, parce que cette autre question suggère que c'est misérable .
Et ma propre contribution, qui est compétitive sur les ordinateurs de bureau, et démontre également une approche qui fonctionne à pleine vitesse sur les systèmes embarqués, contrairement aux algorithmes dépendant du modulo entier:
- Les algorithmes de Ben: http://ideone.com/SsEUW
Si vous souhaitez utiliser ce code, je le mettrai à disposition sous une licence BSD simplifiée (utilisation commerciale autorisée, attribution requise). Il suffit de demander.
Enfin, la fonction ltoa n'est pas standard mais largement disponible.
- version ltoa, pour tous ceux qui ont un compilateur qui le fournit (ideone ne le fait pas): http://ideone.com/T5Wim
Je posterai mes mesures de performance sous forme de réponse sous peu.
Règles pour les algorithmes
- Fournissez le code pour une conversion d'au moins 32 bits signés et non signés en décimaux.
- Produire la sortie sous la forme d'un
std::string. - Aucune astuce incompatible avec le filetage et les signaux (par exemple, les tampons statiques).
- Vous pouvez supposer un jeu de caractères ASCII.
- Assurez-vous de tester votre code sur
INT_MINsur une machine à complément à deux où la valeur absolue n'est pas représentable. - Idéalement, la sortie devrait être caractère pour caractère identique à la version canonique C++ en utilisant
stringstream, http://ideone.com/jh3Sa , mais tout ce qui est clairement compréhensible comme le le bon numéro est ok aussi. - [~ # ~] nouveau [~ # ~] : Bien que vous puissiez utiliser les options de compilation et d'optimisation (sauf complètement désactivées) que vous souhaitez pour la comparaison, le code doit également compiler et donner des résultats corrects sous au moins VC++ 2010 et g ++.
Discussion espérée
Outre de meilleurs algorithmes, j'aimerais également obtenir des références sur plusieurs plates-formes et compilateurs différents (utilisons le débit en Mo/s comme unité de mesure standard). Je crois que le code de mon algorithme (je sais que le benchmark sprintf prend quelques raccourcis - maintenant corrigé) est un comportement bien défini par la norme, au moins sous le ASCII hypothèse, mais si vous voyez un comportement ou des entrées non définis pour lesquels la sortie n'est pas valide, veuillez le signaler.
Conclusions:
Différents algorithmes fonctionnent pour g ++ et VC2010, probablement en raison des différentes implémentations de std::string sur chaque. VC2010 fait clairement un meilleur travail avec NRVO, se débarrasser du retour par valeur n'a aidé que sur gcc.
Il a été constaté que le code surpasse sprintf d'un ordre de grandeur. ostringstream recule d'un facteur 50 et plus.
Le gagnant du défi est user434507 qui produit du code qui exécute 350% de la vitesse de ma propre sur gcc. D'autres entrées sont fermées en raison des caprices de la communauté SO.
Les champions actuels (finaux?) De la vitesse sont:
- Pour gcc: user434507, 8 fois plus rapide que
sprintf: http://ideone.com/0uhhX - Pour Visual C++: Timo, 15 fois plus rapide que
sprintf: http://ideone.com/VpKO
#include <string>
const char digit_pairs[201] = {
"00010203040506070809"
"10111213141516171819"
"20212223242526272829"
"30313233343536373839"
"40414243444546474849"
"50515253545556575859"
"60616263646566676869"
"70717273747576777879"
"80818283848586878889"
"90919293949596979899"
};
std::string& itostr(int n, std::string& s)
{
if(n==0)
{
s="0";
return s;
}
int sign = -(n<0);
unsigned int val = (n^sign)-sign;
int size;
if(val>=10000)
{
if(val>=10000000)
{
if(val>=1000000000)
size=10;
else if(val>=100000000)
size=9;
else
size=8;
}
else
{
if(val>=1000000)
size=7;
else if(val>=100000)
size=6;
else
size=5;
}
}
else
{
if(val>=100)
{
if(val>=1000)
size=4;
else
size=3;
}
else
{
if(val>=10)
size=2;
else
size=1;
}
}
size -= sign;
s.resize(size);
char* c = &s[0];
if(sign)
*c='-';
c += size-1;
while(val>=100)
{
int pos = val % 100;
val /= 100;
*(short*)(c-1)=*(short*)(digit_pairs+2*pos);
c-=2;
}
while(val>0)
{
*c--='0' + (val % 10);
val /= 10;
}
return s;
}
std::string& itostr(unsigned val, std::string& s)
{
if(val==0)
{
s="0";
return s;
}
int size;
if(val>=10000)
{
if(val>=10000000)
{
if(val>=1000000000)
size=10;
else if(val>=100000000)
size=9;
else
size=8;
}
else
{
if(val>=1000000)
size=7;
else if(val>=100000)
size=6;
else
size=5;
}
}
else
{
if(val>=100)
{
if(val>=1000)
size=4;
else
size=3;
}
else
{
if(val>=10)
size=2;
else
size=1;
}
}
s.resize(size);
char* c = &s[size-1];
while(val>=100)
{
int pos = val % 100;
val /= 100;
*(short*)(c-1)=*(short*)(digit_pairs+2*pos);
c-=2;
}
while(val>0)
{
*c--='0' + (val % 10);
val /= 10;
}
return s;
}
Cela explosera sur les systèmes qui interdisent les accès à la mémoire non alignés (dans ce cas, la première affectation non alignée via *(short*) provoquerait une erreur de segmentation), mais devrait fonctionner très bien sinon.
Une chose importante à faire est de minimiser l'utilisation de std::string. (Ironique, je sais.) Dans Visual Studio, par exemple, la plupart des appels aux méthodes de std :: string ne sont pas alignés, même si vous spécifiez/Ob2 dans les options du compilateur. Ainsi, même quelque chose d'aussi banal qu'un appel à std::string::clear(), que vous pourriez attendre très rapidement, peut prendre 100 coups d'horloge lors de la liaison de CRT en tant que bibliothèque statique, et jusqu'à 300 coups d'horloge lors de la liaison en tant que DLL.
Pour la même raison, le retour par référence est préférable car il évite une affectation, un constructeur et un destructeur.
Ah, défi génial au fait ... Je me suis beaucoup amusé avec ça.
J'ai deux algorithmes à soumettre (le code est en bas si vous avez envie de le sauter). Dans mes comparaisons, j'exige que la fonction renvoie une chaîne et qu'elle puisse gérer int et int signé. Comparer des choses qui ne construisent pas une chaîne à celles qui le font n'a pas vraiment de sens.
La première est une implémentation amusante qui n'utilise aucune table de recherche précalculée ni division/modulo explicite. Celui-ci est compétitif avec les autres avec gcc et avec tous sauf Timo sur msvc (pour une bonne raison que j'explique ci-dessous). Le deuxième algorithme est ma soumission réelle pour des performances optimales. Dans mes tests, il bat tous les autres sur gcc et msvc.
Je pense que je sais pourquoi certains des résultats sur MSVC sont très bons. std :: string a deux constructeurs pertinents std::string(char* str, size_t n)
etstd::string(ForwardIterator b, ForwardIterator e)
gcc fait la même chose pour les deux ... c'est-à-dire qu'il utilise le second pour implémenter le premier. Le premier constructeur peut être implémenté de manière beaucoup plus efficace que cela et MSVC le fait. L'avantage secondaire de cela est que dans certains cas (comme mon code rapide et le code de Timo), le constructeur de chaîne peut être intégré. En fait, simplement basculer entre ces constructeurs dans MSVC est presque une différence de 2x pour mon code.
Mes résultats de tests de performance:
Sources de code:
- Voigt
- Timo
- ergosys
- ser434507
- ser-voigt-timo
- hopman-fun
- hopman-fast
gcc 4.4.5 -O2 sur Ubuntu 10.10 64 bits, Core i5
hopman_fun: 124,688 Mo/sec --- 8,020 s hopman_fast: 137,552 Mo/sec --- 7,270 s voigt: 120,192 Mo/sec --- 8,320 s user_voigt_timo: 97,9432 Mo/sec --- 10,210 s timo: 120,482 Mo/sec --- 8,300 s utilisateur: 97,7517 MB/sec --- 10,230 s ergosys: 101,42 Mo/sec --- 9,860 s
MSVC 2010 64 bits/Ox sur Windows 7 64 bits, Core i5
hopman_fun: 127 Mo/sec --- 7.874 s hopman_fast: 259 MB/sec --- 3.861 s voigt: 221.435 MB/sec --- 4.516 s user_voigt_timo: 195,695 Mo/sec --- 5,110 s timo: 253,165 Mo/sec --- 3,950 s utilisateur: 212,63 Mo/sec --- 4,703 s ergosys: 78,0518 Mo/sec --- 12,812 s
Voici quelques résultats et un framework de test/timing sur ideone
http://ideone.com/XZRqp
Notez que ideone est un environnement 32 bits. Mes deux algorithmes en souffrent, mais hopman_fast est au moins toujours compétitif.
Notez que pour ceux qui ne construisent pas une chaîne, j'ai ajouté le modèle de fonction suivant:
template <typename T>
std::string itostr(T t) {
std::string ret;
itostr(t, ret);
return ret;
}
Maintenant, pour mon code ... d'abord le plus amusant:
// hopman_fun
template <typename T>
T reduce2(T v) {
T k = ((v * 410) >> 12) & 0x000F000F000F000Full;
return (((v - k * 10) << 8) + k);
}
template <typename T>
T reduce4(T v) {
T k = ((v * 10486) >> 20) & 0xFF000000FFull;
return reduce2(((v - k * 100) << 16) + (k));
}
typedef unsigned long long ull;
inline ull reduce8(ull v) {
ull k = ((v * 3518437209u) >> 45);
return reduce4(((v - k * 10000) << 32) + (k));
}
template <typename T>
std::string itostr(T o) {
union {
char str[16];
unsigned short u2[8];
unsigned u4[4];
unsigned long long u8[2];
};
unsigned v = o < 0 ? ~o + 1 : o;
u8[0] = (ull(v) * 3518437209u) >> 45;
u8[0] = (u8[0] * 28147497672ull);
u8[1] = v - u2[3] * 100000000;
u8[1] = reduce8(u8[1]);
char* f;
if (u2[3]) {
u2[3] = reduce2(u2[3]);
f = str + 6;
} else {
unsigned short* k = u4[2] ? u2 + 4 : u2 + 6;
f = *k ? (char*)k : (char*)(k + 1);
}
if (!*f) f++;
u4[1] |= 0x30303030;
u4[2] |= 0x30303030;
u4[3] |= 0x30303030;
if (o < 0) *--f = '-';
return std::string(f, (str + 16) - f);
}
Et puis le rapide:
// hopman_fast
struct itostr_helper {
static unsigned out[10000];
itostr_helper() {
for (int i = 0; i < 10000; i++) {
unsigned v = i;
char * o = (char*)(out + i);
o[3] = v % 10 + '0';
o[2] = (v % 100) / 10 + '0';
o[1] = (v % 1000) / 100 + '0';
o[0] = (v % 10000) / 1000;
if (o[0]) o[0] |= 0x30;
else if (o[1] != '0') o[0] |= 0x20;
else if (o[2] != '0') o[0] |= 0x10;
else o[0] |= 0x00;
}
}
};
unsigned itostr_helper::out[10000];
itostr_helper hlp_init;
template <typename T>
std::string itostr(T o) {
typedef itostr_helper hlp;
unsigned blocks[3], *b = blocks + 2;
blocks[0] = o < 0 ? ~o + 1 : o;
blocks[2] = blocks[0] % 10000; blocks[0] /= 10000;
blocks[2] = hlp::out[blocks[2]];
if (blocks[0]) {
blocks[1] = blocks[0] % 10000; blocks[0] /= 10000;
blocks[1] = hlp::out[blocks[1]];
blocks[2] |= 0x30303030;
b--;
}
if (blocks[0]) {
blocks[0] = hlp::out[blocks[0] % 10000];
blocks[1] |= 0x30303030;
b--;
}
char* f = ((char*)b);
f += 3 - (*f >> 4);
char* str = (char*)blocks;
if (o < 0) *--f = '-';
return std::string(f, (str + 12) - f);
}
Données de référence pour le code fourni dans la question:
Sur ideone (gcc 4.3.4):
- flux de chaînes: 4,4 Mo/s
- sprintf: 25,0 Mo/s
- le mien (Ben Voigt) : 55,8 Mo/s
- Timo : 58,5 Mo/s
- ser434507 : 199 Mo/s
- hybride Ben-Timo-507 de user434507 : 263 Mo/s
Core i7, Windows 7 64 bits, 8 Go de RAM, Visual C++ 2010 32 bits:
cl /Ox /EHsc
- flux de chaînes: 3,39 Mo/s, 3,67 Mo/s
- sprintf: 16,8 Mo/s, 16,2 Mo/s
- le mien: 194 Mo/s, 207 Mo/s (avec PGO activé: 250 Mo/s)
Core i7, Windows 7 64 bits, 8 Go de RAM, Visual C++ 2010 64 bits:
cl /Ox /EHsc
- flux de chaînes: 4,42 Mo/s, 4,92 Mo/s
- sprintf: 21,0 Mo/s, 20,8 Mo/s
- le mien: 238 Mo/s, 228 Mo/s
Core i7, Windows 7 64 bits, 8 Go de RAM, cygwin gcc 4.3.4:
g++ -O3
- flux de chaînes: 2,19 Mo/s, 2,17 Mo/s
- sprintf: 13,1 Mo/s, 13,4 Mo/s
- le mien: 30,0 Mo/s, 30,2 Mo/s
edit : J'allais ajouter ma propre réponse, mais la question était fermée, donc je l'ajoute ici. :) J'ai écrit mon propre algorithme et j'ai réussi à obtenir une amélioration décente par rapport au code de Ben, bien que je ne l'ai testé que dans MSVC 2010. J'ai également fait une référence de toutes les implémentations présentées jusqu'à présent, en utilisant la même configuration de test que celle de Ben. code. - Timo
Intel Q9450, Win XP 32 bits, MSVC 2010
cl /O2 /EHsc
- flux de chaîne: 2,87 Mo/s
- sprintf: 16,1 Mo/s
- Ben: 202 Mo/s
- Ben (tampon non signé): 82,0 Mo/s
- ergosys (version mise à jour): 64,2 Mo/s
- user434507: 172 Mo/s
- Timo: 241 Mo/s
-
const char digit_pairs[201] = {
"00010203040506070809"
"10111213141516171819"
"20212223242526272829"
"30313233343536373839"
"40414243444546474849"
"50515253545556575859"
"60616263646566676869"
"70717273747576777879"
"80818283848586878889"
"90919293949596979899"
};
static const int BUFFER_SIZE = 11;
std::string itostr(int val)
{
char buf[BUFFER_SIZE];
char *it = &buf[BUFFER_SIZE-2];
if(val>=0) {
int div = val/100;
while(div) {
memcpy(it,&digit_pairs[2*(val-div*100)],2);
val = div;
it-=2;
div = val/100;
}
memcpy(it,&digit_pairs[2*val],2);
if(val<10)
it++;
} else {
int div = val/100;
while(div) {
memcpy(it,&digit_pairs[-2*(val-div*100)],2);
val = div;
it-=2;
div = val/100;
}
memcpy(it,&digit_pairs[-2*val],2);
if(val<=-10)
it--;
*it = '-';
}
return std::string(it,&buf[BUFFER_SIZE]-it);
}
std::string itostr(unsigned int val)
{
char buf[BUFFER_SIZE];
char *it = (char*)&buf[BUFFER_SIZE-2];
int div = val/100;
while(div) {
memcpy(it,&digit_pairs[2*(val-div*100)],2);
val = div;
it-=2;
div = val/100;
}
memcpy(it,&digit_pairs[2*val],2);
if(val<10)
it++;
return std::string((char*)it,(char*)&buf[BUFFER_SIZE]-(char*)it);
}
Bien que les informations que nous obtenons ici pour les algorithmes soient plutôt agréables, je pense que la question est "cassée", et je vais expliquer pourquoi je pense que ceci:
La question demande de prendre les performances de int-> std::string conversion, et ceci peut être intéressant lors de la comparaison d'une méthode couramment disponible, telle que différentes implémentations stringstream ou boost :: lexical_cast. Cela n'a cependant pas de sens lorsque vous demandez nouveau code, un algorithme spécialisé, pour ce faire. La raison en est que int2string impliquera toujours l'allocation de tas de std :: string et si nous essayons d'extraire le dernier de notre algorithme de conversion, je ne pense pas qu'il soit logique de mélanger ces mesures avec les allocations de tas faites par std: :chaîne. Si je veux une conversion performante, je vais toujours utiliser un tampon de taille fixe et ne jamais allouer quoi que ce soit sur le tas!
Pour résumer, je pense que les horaires devraient être partagés:
- Tout d'abord, la conversion la plus rapide (int -> buffer fixe).
- Deuxièmement, le timing de la copie (tampon fixe -> std :: string).
- Troisièmement, vérifier comment l'allocation std :: string peut directement être utilisée comme tampon, pour enregistrer la copie.
Ces aspects ne doivent pas être mélangés en un seul moment, à mon humble avis.
mis à jour ma réponse ... modp_ufast ...
Integer To String Test (Type 1)
[modp_ufast]Numbers: 240000000 Total: 657777786 Time: 1.1633sec Rate:206308473.0686nums/sec
[sprintf] Numbers: 240000000 Total: 657777786 Time: 24.3629sec Rate: 9851045.8556nums/sec
[karma] Numbers: 240000000 Total: 657777786 Time: 5.2389sec Rate: 45810870.7171nums/sec
[strtk] Numbers: 240000000 Total: 657777786 Time: 3.3126sec Rate: 72450283.7492nums/sec
[so ] Numbers: 240000000 Total: 657777786 Time: 3.0828sec Rate: 77852152.8820nums/sec
[timo ] Numbers: 240000000 Total: 657777786 Time: 4.7349sec Rate: 50687912.9889nums/sec
[voigt] Numbers: 240000000 Total: 657777786 Time: 5.1689sec Rate: 46431985.1142nums/sec
[hopman] Numbers: 240000000 Total: 657777786 Time: 4.6169sec Rate: 51982554.6497nums/sec
Press any key to continue . . .
Integer To String Test(Type 2)
[modp_ufast]Numbers: 240000000 Total: 660000000 Time: 0.5072sec Rate:473162716.4618nums/sec
[sprintf] Numbers: 240000000 Total: 660000000 Time: 22.3483sec Rate: 10739062.9383nums/sec
[karma] Numbers: 240000000 Total: 660000000 Time: 4.2471sec Rate: 56509024.3035nums/sec
[strtk] Numbers: 240000000 Total: 660000000 Time: 2.1683sec Rate:110683636.7123nums/sec
[so ] Numbers: 240000000 Total: 660000000 Time: 2.7133sec Rate: 88454602.1423nums/sec
[timo ] Numbers: 240000000 Total: 660000000 Time: 2.8030sec Rate: 85623453.3872nums/sec
[voigt] Numbers: 240000000 Total: 660000000 Time: 3.4019sec Rate: 70549286.7776nums/sec
[hopman] Numbers: 240000000 Total: 660000000 Time: 2.7849sec Rate: 86178023.8743nums/sec
Press any key to continue . . .
Integer To String Test (type 3)
[modp_ufast]Numbers: 240000000 Total: 505625000 Time: 1.6482sec Rate:145610315.7819nums/sec
[sprintf] Numbers: 240000000 Total: 505625000 Time: 20.7064sec Rate: 11590618.6109nums/sec
[karma] Numbers: 240000000 Total: 505625000 Time: 4.3036sec Rate: 55767734.3570nums/sec
[strtk] Numbers: 240000000 Total: 505625000 Time: 2.9297sec Rate: 81919227.9275nums/sec
[so ] Numbers: 240000000 Total: 505625000 Time: 3.0278sec Rate: 79266003.8158nums/sec
[timo ] Numbers: 240000000 Total: 505625000 Time: 4.0631sec Rate: 59068204.3266nums/sec
[voigt] Numbers: 240000000 Total: 505625000 Time: 4.5616sec Rate: 52613393.0285nums/sec
[hopman] Numbers: 240000000 Total: 505625000 Time: 4.1248sec Rate: 58184194.4569nums/sec
Press any key to continue . . .
int ufast_utoa10(unsigned int value, char* str)
{
#define JOIN(N) N "0", N "1", N "2", N "3", N "4", N "5", N "6", N "7", N "8", N "9"
#define JOIN2(N) JOIN(N "0"), JOIN(N "1"), JOIN(N "2"), JOIN(N "3"), JOIN(N "4"), \
JOIN(N "5"), JOIN(N "6"), JOIN(N "7"), JOIN(N "8"), JOIN(N "9")
#define JOIN3(N) JOIN2(N "0"), JOIN2(N "1"), JOIN2(N "2"), JOIN2(N "3"), JOIN2(N "4"), \
JOIN2(N "5"), JOIN2(N "6"), JOIN2(N "7"), JOIN2(N "8"), JOIN2(N "9")
#define JOIN4 JOIN3("0"), JOIN3("1"), JOIN3("2"), JOIN3("3"), JOIN3("4"), \
JOIN3("5"), JOIN3("6"), JOIN3("7"), JOIN3("8"), JOIN3("9")
#define JOIN5(N) JOIN(N), JOIN(N "1"), JOIN(N "2"), JOIN(N "3"), JOIN(N "4"), \
JOIN(N "5"), JOIN(N "6"), JOIN(N "7"), JOIN(N "8"), JOIN(N "9")
#define JOIN6 JOIN5(), JOIN5("1"), JOIN5("2"), JOIN5("3"), JOIN5("4"), \
JOIN5("5"), JOIN5("6"), JOIN5("7"), JOIN5("8"), JOIN5("9")
#define F(N) ((N) >= 100 ? 3 : (N) >= 10 ? 2 : 1)
#define F10(N) F(N),F(N+1),F(N+2),F(N+3),F(N+4),F(N+5),F(N+6),F(N+7),F(N+8),F(N+9)
#define F100(N) F10(N),F10(N+10),F10(N+20),F10(N+30),F10(N+40),\
F10(N+50),F10(N+60),F10(N+70),F10(N+80),F10(N+90)
static const short offsets[] = { F100(0), F100(100), F100(200), F100(300), F100(400),
F100(500), F100(600), F100(700), F100(800), F100(900)};
static const char table1[][4] = { JOIN("") };
static const char table2[][4] = { JOIN2("") };
static const char table3[][4] = { JOIN3("") };
static const char table4[][5] = { JOIN4 };
static const char table5[][4] = { JOIN6 };
#undef JOIN
#undef JOIN2
#undef JOIN3
#undef JOIN4
char *wstr;
int remains[2];
unsigned int v2;
if (value >= 100000000) {
v2 = value / 10000;
remains[0] = value - v2 * 10000;
value = v2;
v2 = value / 10000;
remains[1] = value - v2 * 10000;
value = v2;
wstr = str;
if (value >= 1000) {
*(__int32 *) wstr = *(__int32 *) table4[value];
wstr += 4;
} else {
*(__int32 *) wstr = *(__int32 *) table5[value];
wstr += offsets[value];
}
*(__int32 *) wstr = *(__int32 *) table4[remains[1]];
wstr += 4;
*(__int32 *) wstr = *(__int32 *) table4[remains[0]];
wstr += 4;
*wstr = 0;
return (wstr - str);
}
else if (value >= 10000) {
v2 = value / 10000;
remains[0] = value - v2 * 10000;
value = v2;
wstr = str;
if (value >= 1000) {
*(__int32 *) wstr = *(__int32 *) table4[value];
wstr += 4;
*(__int32 *) wstr = *(__int32 *) table4[remains[0]];
wstr += 4;
*wstr = 0;
return 8;
} else {
*(__int32 *) wstr = *(__int32 *) table5[value];
wstr += offsets[value];
*(__int32 *) wstr = *(__int32 *) table4[remains[0]];
wstr += 4;
*wstr = 0;
return (wstr - str);
}
}
else {
if (value >= 1000) {
*(__int32 *) str = *(__int32 *) table4[value];
str += 4;
*str = 0;
return 4;
} else if (value >= 100) {
*(__int32 *) str = *(__int32 *) table3[value];
return 3;
} else if (value >= 10) {
*(__int16 *) str = *(__int16 *) table2[value];
str += 2;
*str = 0;
return 2;
} else {
*(__int16 *) str = *(__int16 *) table1[value];
return 1;
}
}
}
int ufast_itoa10(int value, char* str) {
if (value < 0) { *(str++) = '-';
return ufast_utoa10(-value, str) + 1;
}
else return ufast_utoa10(value, str);
}
void ufast_test() {
print_mode("[modp_ufast]");
std::string s;
s.reserve(32);
std::size_t total_length = 0;
strtk::util::timer t;
t.start();
char buf[128];
int len;
for (int i = (-max_i2s / 2); i < (max_i2s / 2); ++i)
{
#ifdef enable_test_type01
s.resize(ufast_itoa10(((i & 1) ? i : -i), const_cast<char*>(s.c_str())));
total_length += s.size();
#endif
#ifdef enable_test_type02
s.resize(ufast_itoa10(max_i2s + i, const_cast<char*>(s.c_str())));
total_length += s.size();
#endif
#ifdef enable_test_type03
s.resize(ufast_itoa10(randval[(max_i2s + i) & 1023], const_cast<char*>(s.c_str())));
total_length += s.size();
#endif
}
t.stop();
printf("Numbers:%10lu\tTotal:%12lu\tTime:%8.4fsec\tRate:%14.4fnums/sec\n",
static_cast<unsigned long>(3 * max_i2s),
static_cast<unsigned long>(total_length),
t.time(),
(3.0 * max_i2s) / t.time());
}
Je ne peux pas tester sous VS, mais cela semble être plus rapide que votre code pour g ++, environ 10%. Il pourrait probablement être réglé, les valeurs de décision choisies sont des suppositions. int seulement, désolé.
typedef unsigned buf_t;
static buf_t * reduce(unsigned val, buf_t * stp) {
unsigned above = val / 10000;
if (above != 0) {
stp = reduce(above, stp);
val -= above * 10000;
}
buf_t digit = val / 1000;
*stp++ = digit + '0';
val -= digit * 1000;
digit = val / 100;
*stp++ = digit + '0';
val -= digit * 100;
digit = val / 10;
*stp++ = digit + '0';
val -= digit * 10;
*stp++ = val + '0';
return stp;
}
std::string itostr(int input) {
buf_t buf[16];
if(input == INT_MIN) {
char buf2[16];
std::sprintf(buf2, "%d", input);
return std::string(buf2);
}
// handle negative
unsigned val = input;
if(input < 0)
val = -input;
buf[0] = '0';
buf_t* endp = reduce(val, buf+1);
*endp = 127;
buf_t * stp = buf+1;
while (*stp == '0')
stp++;
if (stp == endp)
stp--;
if (input < 0) {
stp--;
*stp = '-';
}
return std::string(stp, endp);
}
Voici ma petite tentative de ce puzzle amusant.
Au lieu d'utiliser des tables de recherche, je voulais que le compilateur comprenne tout cela. Dans ce cas en particulier - si vous lisez Hackers 'Delight, vous voyez comment diviser et modulo fonctionnent - ce qui rend très possible l'optimisation à l'aide des instructions SSE/AVX.
Référence de performance
En ce qui concerne la vitesse, mon indice de référence ici me dit qu'il est 1,5 fois plus rapide que le travail de Timo (sur mon Intel Haswell, il fonctionne à environ 1 Go/s).
Choses que vous pourriez considérer comme une triche
En ce qui concerne la triche de non-fabrication d'une chaîne std que j'utilise - bien sûr, j'ai pris cela en considération pour ma référence de la méthode de Timo.
J'utilise un intrinsèque: BSR. Si vous le souhaitez, vous pouvez également utiliser des tables DeBruijn à la place - ce qui est l'une des choses que j'ai écrites un peu sur mon article "2log le plus rapide". Bien sûr, cela a une pénalité de performance (* eh bien ... si vous faites beaucoup d'opérations itoa, vous pouvez réellement faire un BSR plus rapide mais je suppose que ce n'est pas juste ...).
La façon dont cela fonctionne
La première chose à faire est de déterminer la quantité de mémoire dont nous avons besoin. Il s'agit essentiellement d'un 10log, qui peut être implémenté de plusieurs façons intelligentes. Voir le " Bit Twiddling Hacks " fréquemment cité pour plus de détails.
La prochaine chose à faire est d'exécuter la sortie numérique. J'utilise la récursivité du modèle pour cela, donc le compilateur le comprendra.
J'utilise "modulo" et "div" côte à côte. Si vous lisez Hacker's Delight, vous remarquerez que les deux sont étroitement liés, donc si vous avez une réponse, vous avez probablement aussi l'autre. J'ai pensé que le compilateur pouvait comprendre les détails ... :-)
Le code
Obtenir le nombre de chiffres à l'aide d'un journal (modifié) 10:
struct logarithm
{
static inline int log2(unsigned int value)
{
unsigned long index;
if (!_BitScanReverse(&index, value))
{
return 0;
}
// add 1 if x is NOT a power of 2 (to do the ceil)
return index + (value&(value - 1) ? 1 : 0);
}
static inline int numberDigits(unsigned int v)
{
static unsigned int const PowersOf10[] =
{ 0, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000 };
int t = (logarithm::log2(v) + 1) * 1233 >> 12; // (use a lg2 method from above)
return 1 + t - (v < PowersOf10[t]);
}
};
Se procurer la chaîne:
template <int count>
struct WriteHelper
{
inline static void WriteChar(char* buf, unsigned int value)
{
unsigned int div = value / 10;
unsigned int rem = value % 10;
buf[count - 1] = rem + '0';
WriteHelper<count - 1>::WriteChar(buf, div);
}
};
template <>
struct WriteHelper<1>
{
inline static void WriteChar(char* buf, unsigned int value)
{
buf[0] = '0' + value;
}
};
// Boring code that converts a length into a switch.
// TODO: Test if recursion with an 'if' is faster.
static inline void WriteNumber(char* data, int len, unsigned int val)
{
switch (len) {
case 1:
WriteHelper<1>::WriteChar(data, static_cast<unsigned int>(val));
break;
case 2:
WriteHelper<2>::WriteChar(data, static_cast<unsigned int>(val));
break;
case 3:
WriteHelper<3>::WriteChar(data, static_cast<unsigned int>(val));
break;
case 4:
WriteHelper<4>::WriteChar(data, static_cast<unsigned int>(val));
break;
case 5:
WriteHelper<5>::WriteChar(data, static_cast<unsigned int>(val));
break;
case 6:
WriteHelper<6>::WriteChar(data, static_cast<unsigned int>(val));
break;
case 7:
WriteHelper<7>::WriteChar(data, static_cast<unsigned int>(val));
break;
case 8:
WriteHelper<8>::WriteChar(data, static_cast<unsigned int>(val));
break;
case 9:
WriteHelper<9>::WriteChar(data, static_cast<unsigned int>(val));
break;
case 10:
WriteHelper<10>::WriteChar(data, static_cast<unsigned int>(val));
break;
}
}
// The main method you want to call...
static int Write(char* data, int val)
{
int len;
if (val >= 0)
{
len = logarithm::numberDigits(val);
WriteNumber(data, len, unsigned int(val));
return len;
}
else
{
unsigned int v(-val);
len = logarithm::numberDigits(v);
WriteNumber(data+1, len, v);
data[0] = '-';
return len + 1;
}
}
Je l'ai depuis longtemps assis et j'ai finalement réussi à le poster.
Quelques méthodes supplémentaires par rapport au double-mot à la fois hopman_fast. Les résultats sont pour la chaîne std :: string optimisée pour les chaînes courtes, car sinon les différences de performances sont masquées par la surcharge du code de gestion des chaînes de copie sur écriture. Le débit est mesuré de la même manière qu'ailleurs dans cette rubrique, le nombre de cycles concerne les parties de sérialisation brutes du code avant de copier le tampon de sortie dans une chaîne.
HOPMAN_FAST - performance reference
TM_CPP, TM_VEC - scalar and vector versions of Terje Mathisen algorithm
WM_VEC - intrinsics implementation of Wojciech Mula's vector algorithm
AK_BW - Word-at-a-time routine with a jump table that fills a buffer in reverse
AK_FW - forward-stepping Word-at-a-time routine with a jump table in Assembly
AK_UNROLLED - generic Word-at-a-time routine that uses an unrolled loop
Commutateurs de compilation:
-DVSTRING - active les chaînes SSO pour les anciennes configurations GCC
- DBSR1 - permet une journalisation rapide10
- DRDTSC - active les compteurs de cycles
#include <cstdio>
#include <iostream>
#include <climits>
#include <sstream>
#include <algorithm>
#include <cstring>
#include <limits>
#include <ctime>
#include <stdint.h>
#include <x86intrin.h>
/* Uncomment to run */
// #define HOPMAN_FAST
// #define TM_CPP
// #define TM_VEC
// #define WM_VEC
// #define AK_UNROLLED
// #define AK_BW
// #define AK_FW
using namespace std;
#ifdef VSTRING
#include <ext/vstring.h>
typedef __gnu_cxx::__vstring string_type;
#else
typedef string string_type;
#endif
namespace detail {
#ifdef __GNUC__
#define ALIGN(N) __attribute__ ((aligned(N)))
#define PACK __attribute__ ((packed))
inline size_t num_digits(unsigned u) {
struct {
uint32_t count;
uint32_t max;
} static digits[32] ALIGN(64) = {
{ 1, 9 }, { 1, 9 }, { 1, 9 }, { 1, 9 },
{ 2, 99 }, { 2, 99 }, { 2, 99 },
{ 3, 999 }, { 3, 999 }, { 3, 999 },
{ 4, 9999 }, { 4, 9999 }, { 4, 9999 }, { 4, 9999 },
{ 5, 99999 }, { 5, 99999 }, { 5, 99999 },
{ 6, 999999 }, { 6, 999999 }, { 6, 999999 },
{ 7, 9999999 }, { 7, 9999999 }, { 7, 9999999 }, { 7, 9999999 },
{ 8, 99999999 }, { 8, 99999999 }, { 8, 99999999 },
{ 9, 999999999 }, { 9, 999999999 }, { 9, 999999999 },
{ 10, UINT_MAX }, { 10, UINT_MAX }
};
#if (defined(i386) || defined(__x86_64__)) && (defined(BSR1) || defined(BSR2))
size_t l = u;
#if defined(BSR1)
__asm__ __volatile__ (
"bsrl %k0, %k0 \n\t"
"shlq $32, %q1 \n\t"
"movq %c2(,%0,8), %0\n\t"
"cmpq %0, %q1 \n\t"
"seta %b1 \n\t"
"addl %1, %k0 \n\t"
: "+r" (l), "+r"(u)
: "i"(digits)
: "cc"
);
return l;
#else
__asm__ __volatile__ ( "bsr %0, %0;" : "+r" (l) );
return digits[l].count + ( u > digits[l].max );
#endif
#else
size_t l = (u != 0) ? 31 - __builtin_clz(u) : 0;
return digits[l].count + ( u > digits[l].max );
#endif
}
#else
inline unsigned msb_u32(unsigned x) {
static const unsigned bval[] = { 0,1,2,2,3,3,3,3,4,4,4,4,4,4,4,4 };
unsigned base = 0;
if (x & (unsigned) 0xFFFF0000) { base += 32/2; x >>= 32/2; }
if (x & (unsigned) 0x0000FF00) { base += 32/4; x >>= 32/4; }
if (x & (unsigned) 0x000000F0) { base += 32/8; x >>= 32/8; }
return base + bval[x];
}
inline size_t num_digits(unsigned x) {
static const unsigned powertable[] = {
0,10,100,1000,10000,100000,1000000,10000000,100000000, 1000000000 };
size_t lg_ten = msb_u32(x) * 1233 >> 12;
size_t adjust = (x >= powertable[lg_ten]);
return lg_ten + adjust;
}
#endif /* __GNUC__ */
struct CharBuffer {
class reverse_iterator : public iterator<random_access_iterator_tag, char> {
char* m_p;
public:
reverse_iterator(char* p) : m_p(p - 1) {}
reverse_iterator operator++() { return --m_p; }
reverse_iterator operator++(int) { return m_p--; }
char operator*() const { return *m_p; }
bool operator==( reverse_iterator it) const { return m_p == it.m_p; }
bool operator!=( reverse_iterator it) const { return m_p != it.m_p; }
difference_type operator-( reverse_iterator it) const { return it.m_p - m_p; }
};
};
union PairTable {
char c[2];
unsigned short u;
} PACK table[100] ALIGN(1024) = {
{{'0','0'}},{{'0','1'}},{{'0','2'}},{{'0','3'}},{{'0','4'}},{{'0','5'}},{{'0','6'}},{{'0','7'}},{{'0','8'}},{{'0','9'}},
{{'1','0'}},{{'1','1'}},{{'1','2'}},{{'1','3'}},{{'1','4'}},{{'1','5'}},{{'1','6'}},{{'1','7'}},{{'1','8'}},{{'1','9'}},
{{'2','0'}},{{'2','1'}},{{'2','2'}},{{'2','3'}},{{'2','4'}},{{'2','5'}},{{'2','6'}},{{'2','7'}},{{'2','8'}},{{'2','9'}},
{{'3','0'}},{{'3','1'}},{{'3','2'}},{{'3','3'}},{{'3','4'}},{{'3','5'}},{{'3','6'}},{{'3','7'}},{{'3','8'}},{{'3','9'}},
{{'4','0'}},{{'4','1'}},{{'4','2'}},{{'4','3'}},{{'4','4'}},{{'4','5'}},{{'4','6'}},{{'4','7'}},{{'4','8'}},{{'4','9'}},
{{'5','0'}},{{'5','1'}},{{'5','2'}},{{'5','3'}},{{'5','4'}},{{'5','5'}},{{'5','6'}},{{'5','7'}},{{'5','8'}},{{'5','9'}},
{{'6','0'}},{{'6','1'}},{{'6','2'}},{{'6','3'}},{{'6','4'}},{{'6','5'}},{{'6','6'}},{{'6','7'}},{{'6','8'}},{{'6','9'}},
{{'7','0'}},{{'7','1'}},{{'7','2'}},{{'7','3'}},{{'7','4'}},{{'7','5'}},{{'7','6'}},{{'7','7'}},{{'7','8'}},{{'7','9'}},
{{'8','0'}},{{'8','1'}},{{'8','2'}},{{'8','3'}},{{'8','4'}},{{'8','5'}},{{'8','6'}},{{'8','7'}},{{'8','8'}},{{'8','9'}},
{{'9','0'}},{{'9','1'}},{{'9','2'}},{{'9','3'}},{{'9','4'}},{{'9','5'}},{{'9','6'}},{{'9','7'}},{{'9','8'}},{{'9','9'}}
};
} // namespace detail
struct progress_timer {
clock_t c;
progress_timer() : c(clock()) {}
int elapsed() { return clock() - c; }
~progress_timer() {
clock_t d = clock() - c;
cout << d / CLOCKS_PER_SEC << "."
<< (((d * 1000) / CLOCKS_PER_SEC) % 1000 / 100)
<< (((d * 1000) / CLOCKS_PER_SEC) % 100 / 10)
<< (((d * 1000) / CLOCKS_PER_SEC) % 10)
<< " s" << endl;
}
};
#ifdef HOPMAN_FAST
namespace hopman_fast {
static unsigned long cpu_cycles = 0;
struct itostr_helper {
static ALIGN(1024) unsigned out[10000];
itostr_helper() {
for (int i = 0; i < 10000; i++) {
unsigned v = i;
char * o = (char*)(out + i);
o[3] = v % 10 + '0';
o[2] = (v % 100) / 10 + '0';
o[1] = (v % 1000) / 100 + '0';
o[0] = (v % 10000) / 1000;
if (o[0]) o[0] |= 0x30;
else if (o[1] != '0') o[0] |= 0x20;
else if (o[2] != '0') o[0] |= 0x10;
else o[0] |= 0x00;
}
}
};
unsigned itostr_helper::out[10000];
itostr_helper hlp_init;
template <typename T>
string_type itostr(T o) {
typedef itostr_helper hlp;
#ifdef RDTSC
long first_clock = __rdtsc();
#endif
unsigned blocks[3], *b = blocks + 2;
blocks[0] = o < 0 ? ~o + 1 : o;
blocks[2] = blocks[0] % 10000; blocks[0] /= 10000;
blocks[2] = hlp::out[blocks[2]];
if (blocks[0]) {
blocks[1] = blocks[0] % 10000; blocks[0] /= 10000;
blocks[1] = hlp::out[blocks[1]];
blocks[2] |= 0x30303030;
b--;
}
if (blocks[0]) {
blocks[0] = hlp::out[blocks[0] % 10000];
blocks[1] |= 0x30303030;
b--;
}
char* f = ((char*)b);
f += 3 - (*f >> 4);
char* str = (char*)blocks;
if (o < 0) *--f = '-';
str += 12;
#ifdef RDTSC
cpu_cycles += __rdtsc() - first_clock;
#endif
return string_type(f, str);
}
unsigned long cycles() { return cpu_cycles; }
void reset() { cpu_cycles = 0; }
}
#endif
namespace ak {
#ifdef AK_UNROLLED
namespace unrolled {
static unsigned long cpu_cycles = 0;
template <typename value_type> class Proxy {
static const size_t MaxValueSize = 16;
static inline char* generate(int value, char* buffer) {
union { char* pc; unsigned short* pu; } b = { buffer + MaxValueSize };
unsigned u, v = value < 0 ? unsigned(~value) + 1 : value;
*--b.pu = detail::table[v % 100].u; u = v;
if ((v /= 100)) {
*--b.pu = detail::table[v % 100].u; u = v;
if ((v /= 100)) {
*--b.pu = detail::table[v % 100].u; u = v;
if ((v /= 100)) {
*--b.pu = detail::table[v % 100].u; u = v;
if ((v /= 100)) {
*--b.pu = detail::table[v % 100].u; u = v;
} } } }
*(b.pc -= (u >= 10)) = '-';
return b.pc + (value >= 0);
}
static inline char* generate(unsigned value, char* buffer) {
union { char* pc; unsigned short* pu; } b = { buffer + MaxValueSize };
unsigned u, v = value;
*--b.pu = detail::table[v % 100].u; u = v;
if ((v /= 100)) {
*--b.pu = detail::table[v % 100].u; u = v;
if ((v /= 100)) {
*--b.pu = detail::table[v % 100].u; u = v;
if ((v /= 100)) {
*--b.pu = detail::table[v % 100].u; u = v;
if ((v /= 100)) {
*--b.pu = detail::table[v % 100].u; u = v;
} } } }
return b.pc + (u < 10);
}
public:
static inline string_type convert(value_type v) {
char buf[MaxValueSize];
#ifdef RDTSC
long first_clock = __rdtsc();
#endif
char* p = generate(v, buf);
char* e = buf + MaxValueSize;
#ifdef RDTSC
cpu_cycles += __rdtsc() - first_clock;
#endif
return string_type(p, e);
}
};
string_type itostr(int i) { return Proxy<int>::convert(i); }
string_type itostr(unsigned i) { return Proxy<unsigned>::convert(i); }
unsigned long cycles() { return cpu_cycles; }
void reset() { cpu_cycles = 0; }
}
#endif
#if defined(AK_BW)
namespace bw {
static unsigned long cpu_cycles = 0;
typedef uint64_t u_type;
template <typename value_type> class Proxy {
static inline void generate(unsigned v, size_t len, char* buffer) {
u_type u = v;
switch(len) {
default: u = (v * 1374389535ULL) >> 37; *(uint16_t*)(buffer + 8) = detail::table[v -= 100 * u].u;
case 8: v = (u * 1374389535ULL) >> 37; *(uint16_t*)(buffer + 6) = detail::table[u -= 100 * v].u;
case 6: u = (v * 1374389535ULL) >> 37; *(uint16_t*)(buffer + 4) = detail::table[v -= 100 * u].u;
case 4: v = (u * 167773) >> 24; *(uint16_t*)(buffer + 2) = detail::table[u -= 100 * v].u;
case 2: *(uint16_t*)buffer = detail::table[v].u;
case 0: return;
case 9: u = (v * 1374389535ULL) >> 37; *(uint16_t*)(buffer + 7) = detail::table[v -= 100 * u].u;
case 7: v = (u * 1374389535ULL) >> 37; *(uint16_t*)(buffer + 5) = detail::table[u -= 100 * v].u;
case 5: u = (v * 1374389535ULL) >> 37; *(uint16_t*)(buffer + 3) = detail::table[v -= 100 * u].u;
case 3: v = (u * 167773) >> 24; *(uint16_t*)(buffer + 1) = detail::table[u -= 100 * v].u;
case 1: *buffer = v + 0x30;
}
}
public:
static inline string_type convert(bool neg, unsigned val) {
char buf[16];
#ifdef RDTSC
long first_clock = __rdtsc();
#endif
size_t len = detail::num_digits(val);
buf[0] = '-';
char* e = buf + neg;
generate(val, len, e);
e += len;
#ifdef RDTSC
cpu_cycles += __rdtsc() - first_clock;
#endif
return string_type(buf, e);
}
};
string_type itostr(int i) { return Proxy<int>::convert(i < 0, i < 0 ? unsigned(~i) + 1 : i); }
string_type itostr(unsigned i) { return Proxy<unsigned>::convert(false, i); }
unsigned long cycles() { return cpu_cycles; }
void reset() { cpu_cycles = 0; }
}
#endif
#if defined(AK_FW)
namespace fw {
static unsigned long cpu_cycles = 0;
typedef uint32_t u_type;
template <typename value_type> class Proxy {
static inline void generate(unsigned v, size_t len, char* buffer) {
#if defined(__GNUC__) && defined(__x86_64__)
uint16_t w;
uint32_t u;
__asm__ __volatile__ (
"jmp %*T%=(,%3,8) \n\t"
"T%=: .quad L0%= \n\t"
" .quad L1%= \n\t"
" .quad L2%= \n\t"
" .quad L3%= \n\t"
" .quad L4%= \n\t"
" .quad L5%= \n\t"
" .quad L6%= \n\t"
" .quad L7%= \n\t"
" .quad L8%= \n\t"
" .quad L9%= \n\t"
" .quad L10%= \n\t"
"L10%=: \n\t"
" imulq $1441151881, %q0, %q1\n\t"
" shrq $57, %q1 \n\t"
" movw %c5(,%q1,2), %w2 \n\t"
" imull $100000000, %1, %1 \n\t"
" subl %1, %0 \n\t"
" movw %w2, (%4) \n\t"
"L8%=: \n\t"
" imulq $1125899907, %q0, %q1\n\t"
" shrq $50, %q1 \n\t"
" movw %c5(,%q1,2), %w2 \n\t"
" imull $1000000, %1, %1 \n\t"
" subl %1, %0 \n\t"
" movw %w2, -8(%4,%3) \n\t"
"L6%=: \n\t"
" imulq $429497, %q0, %q1 \n\t"
" shrq $32, %q1 \n\t"
" movw %c5(,%q1,2), %w2 \n\t"
" imull $10000, %1, %1 \n\t"
" subl %1, %0 \n\t"
" movw %w2, -6(%4,%3) \n\t"
"L4%=: \n\t"
" imull $167773, %0, %1 \n\t"
" shrl $24, %1 \n\t"
" movw %c5(,%q1,2), %w2 \n\t"
" imull $100, %1, %1 \n\t"
" subl %1, %0 \n\t"
" movw %w2, -4(%4,%3) \n\t"
"L2%=: \n\t"
" movw %c5(,%q0,2), %w2 \n\t"
" movw %w2, -2(%4,%3) \n\t"
"L0%=: jmp 1f \n\t"
"L9%=: \n\t"
" imulq $1801439851, %q0, %q1\n\t"
" shrq $54, %q1 \n\t"
" movw %c5(,%q1,2), %w2 \n\t"
" imull $10000000, %1, %1 \n\t"
" subl %1, %0 \n\t"
" movw %w2, (%4) \n\t"
"L7%=: \n\t"
" imulq $43980466, %q0, %q1 \n\t"
" shrq $42, %q1 \n\t"
" movw %c5(,%q1,2), %w2 \n\t"
" imull $100000, %1, %1 \n\t"
" subl %1, %0 \n\t"
" movw %w2, -7(%4,%3) \n\t"
"L5%=: \n\t"
" imulq $268436, %q0, %q1 \n\t"
" shrq $28, %q1 \n\t"
" movw %c5(,%q1,2), %w2 \n\t"
" imull $1000, %1, %1 \n\t"
" subl %1, %0 \n\t"
" movw %w2, -5(%4,%3) \n\t"
"L3%=: \n\t"
" imull $6554, %0, %1 \n\t"
" shrl $15, %1 \n\t"
" andb $254, %b1 \n\t"
" movw %c5(,%q1), %w2 \n\t"
" leal (%1,%1,4), %1 \n\t"
" subl %1, %0 \n\t"
" movw %w2, -3(%4,%3) \n\t"
"L1%=: \n\t"
" addl $48, %0 \n\t"
" movb %b0, -1(%4,%3) \n\t"
"1: \n\t"
: "+r"(v), "=&q"(u), "=&r"(w)
: "r"(len), "r"(buffer), "i"(detail::table)
: "memory", "cc"
);
#else
u_type u;
switch(len) {
default: u = (v * 1441151881ULL) >> 57; *(uint16_t*)(buffer) = detail::table[u].u; v -= u * 100000000;
case 8: u = (v * 1125899907ULL) >> 50; *(uint16_t*)(buffer + len - 8) = detail::table[u].u; v -= u * 1000000;
case 6: u = (v * 429497ULL) >> 32; *(uint16_t*)(buffer + len - 6) = detail::table[u].u; v -= u * 10000;
case 4: u = (v * 167773) >> 24; *(uint16_t*)(buffer + len - 4) = detail::table[u].u; v -= u * 100;
case 2: *(uint16_t*)(buffer + len - 2) = detail::table[v].u;
case 0: return;
case 9: u = (v * 1801439851ULL) >> 54; *(uint16_t*)(buffer) = detail::table[u].u; v -= u * 10000000;
case 7: u = (v * 43980466ULL) >> 42; *(uint16_t*)(buffer + len - 7) = detail::table[u].u; v -= u * 100000;
case 5: u = (v * 268436ULL) >> 28; *(uint16_t*)(buffer + len - 5) = detail::table[u].u; v -= u * 1000;
case 3: u = (v * 6554) >> 16; *(uint16_t*)(buffer + len - 3) = detail::table[u].u; v -= u * 10;
case 1: *(buffer + len - 1) = v + 0x30;
}
#endif
}
public:
static inline string_type convert(bool neg, unsigned val) {
char buf[16];
#ifdef RDTSC
long first_clock = __rdtsc();
#endif
size_t len = detail::num_digits(val);
if (neg) buf[0] = '-';
char* e = buf + len + neg;
generate(val, len, buf + neg);
#ifdef RDTSC
cpu_cycles += __rdtsc() - first_clock;
#endif
return string_type(buf, e);
}
};
string_type itostr(int i) { return Proxy<int>::convert(i < 0, i < 0 ? unsigned(~i) + 1 : i); }
string_type itostr(unsigned i) { return Proxy<unsigned>::convert(false, i); }
unsigned long cycles() { return cpu_cycles; }
void reset() { cpu_cycles = 0; }
}
#endif
} // ak
namespace wm {
#ifdef WM_VEC
#if defined(__GNUC__) && defined(__x86_64__)
namespace vec {
static unsigned long cpu_cycles = 0;
template <typename value_type> class Proxy {
static inline unsigned generate(unsigned v, char* buf) {
static struct {
unsigned short mul_10[8];
unsigned short div_const[8];
unsigned short shl_const[8];
unsigned char to_ascii[16];
} ALIGN(64) bits =
{
{ // mul_10
10, 10, 10, 10, 10, 10, 10, 10
},
{ // div_const
8389, 5243, 13108, 0x8000, 8389, 5243, 13108, 0x8000
},
{ // shl_const
1 << (16 - (23 + 2 - 16)),
1 << (16 - (19 + 2 - 16)),
1 << (16 - 1 - 2),
1 << (15),
1 << (16 - (23 + 2 - 16)),
1 << (16 - (19 + 2 - 16)),
1 << (16 - 1 - 2),
1 << (15)
},
{ // to_ascii
'0', '0', '0', '0', '0', '0', '0', '0',
'0', '0', '0', '0', '0', '0', '0', '0'
}
};
unsigned x, y, l;
x = (v * 1374389535ULL) >> 37;
y = v;
l = 0;
if (x) {
unsigned div = 0xd1b71759;
unsigned mul = 55536;
__m128i z, m, a, o;
y -= 100 * x;
z = _mm_cvtsi32_si128(x);
m = _mm_load_si128((__m128i*)bits.mul_10);
o = _mm_mul_epu32( z, _mm_cvtsi32_si128(div));
z = _mm_add_epi32( z, _mm_mul_epu32( _mm_cvtsi32_si128(mul), _mm_srli_epi64( o, 45) ) );
z = _mm_slli_epi64( _mm_shuffle_epi32( _mm_unpacklo_epi16(z, z), 5 ), 2 );
a = _mm_load_si128((__m128i*)bits.to_ascii);
z = _mm_mulhi_epu16( _mm_mulhi_epu16( z, *(__m128i*)bits.div_const ), *(__m128i*)bits.shl_const );
z = _mm_sub_epi16( z, _mm_slli_epi64( _mm_mullo_epi16( m, z ), 16 ) );
z = _mm_add_epi8( _mm_packus_epi16( z, _mm_xor_si128(o, o) ), a );
x = __builtin_ctz( ~_mm_movemask_epi8( _mm_cmpeq_epi8( a, z ) ) );
l = 8 - x;
uint64_t q = _mm_cvtsi128_si64(z) >> (x * 8);
*(uint64_t*)buf = q;
buf += l;
x = 1;
}
v = (y * 6554) >> 16;
l += 1 + (x | (v != 0));
*(unsigned short*)buf = 0x30 + ((l > 1) ? ((0x30 + y - v * 10) << 8) + v : y);
return l;
}
public:
static inline string_type convert(bool neg, unsigned val) {
char buf[16];
#ifdef RDTSC
long first_clock = __rdtsc();
#endif
buf[0] = '-';
unsigned len = generate(val, buf + neg);
char* e = buf + len + neg;
#ifdef RDTSC
cpu_cycles += __rdtsc() - first_clock;
#endif
return string_type(buf, e);
}
};
inline string_type itostr(int i) { return Proxy<int>::convert(i < 0, i < 0 ? unsigned(~i) + 1 : i); }
inline string_type itostr(unsigned i) { return Proxy<unsigned>::convert(false, i); }
unsigned long cycles() { return cpu_cycles; }
void reset() { cpu_cycles = 0; }
}
#endif
#endif
} // wm
namespace tmn {
#ifdef TM_CPP
namespace cpp {
static unsigned long cpu_cycles = 0;
template <typename value_type> class Proxy {
static inline void generate(unsigned v, char* buffer) {
unsigned const f1_10000 = (1 << 28) / 10000;
unsigned tmplo, tmphi;
unsigned lo = v % 100000;
unsigned hi = v / 100000;
tmplo = lo * (f1_10000 + 1) - (lo >> 2);
tmphi = hi * (f1_10000 + 1) - (hi >> 2);
unsigned mask = 0x0fffffff;
unsigned shift = 28;
for(size_t i = 0; i < 5; i++)
{
buffer[i + 0] = '0' + (char)(tmphi >> shift);
buffer[i + 5] = '0' + (char)(tmplo >> shift);
tmphi = (tmphi & mask) * 5;
tmplo = (tmplo & mask) * 5;
mask >>= 1;
shift--;
}
}
public:
static inline string_type convert(bool neg, unsigned val) {
#ifdef RDTSC
long first_clock = __rdtsc();
#endif
char buf[16];
size_t len = detail::num_digits(val);
char* e = buf + 11;
generate(val, buf + 1);
buf[10 - len] = '-';
len += neg;
char* b = e - len;
#ifdef RDTSC
cpu_cycles += __rdtsc() - first_clock;
#endif
return string_type(b, e);
}
};
string_type itostr(int i) { return Proxy<int>::convert(i < 0, i < 0 ? unsigned(~i) + 1 : i); }
string_type itostr(unsigned i) { return Proxy<unsigned>::convert(false, i); }
unsigned long cycles() { return cpu_cycles; }
void reset() { cpu_cycles = 0; }
}
#endif
#ifdef TM_VEC
namespace vec {
static unsigned long cpu_cycles = 0;
template <typename value_type> class Proxy {
static inline unsigned generate(unsigned val, char* buffer) {
static struct {
unsigned char mul_10[16];
unsigned char to_ascii[16];
unsigned char gather[16];
unsigned char shift[16];
} ALIGN(64) bits = {
{ 10,0,0,0,10,0,0,0,10,0,0,0,10,0,0,0 },
{ '0','0','0','0','0','0','0','0','0','0','0','0','0','0','0','0' },
{ 3,5,6,7,9,10,11,13,14,15,0,0,0,0,0,0 },
{ 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 }
};
unsigned u = val / 1000000;
unsigned l = val - u * 1000000;
__m128i x, h, f, m, n;
n = _mm_load_si128((__m128i*)bits.mul_10);
x = _mm_set_epi64x( l, u );
h = _mm_mul_epu32( x, _mm_set1_epi32(4294968) );
x = _mm_sub_epi64( x, _mm_srli_epi64( _mm_mullo_epi32( h, _mm_set1_epi32(1000) ), 32 ) );
f = _mm_set1_epi32((1 << 28) / 1000 + 1);
m = _mm_srli_epi32( _mm_cmpeq_epi32(m, m), 4 );
x = _mm_shuffle_epi32( _mm_blend_epi16( x, h, 204 ), 177 );
f = _mm_sub_epi32( _mm_mullo_epi32(f, x), _mm_srli_epi32(x, 2) );
h = _mm_load_si128((__m128i*)bits.to_ascii);
x = _mm_srli_epi32(f, 28);
f = _mm_mullo_epi32( _mm_and_si128( f, m ), n );
x = _mm_or_si128( x, _mm_slli_epi32(_mm_srli_epi32(f, 28), 8) );
f = _mm_mullo_epi32( _mm_and_si128( f, m ), n );
x = _mm_or_si128( x, _mm_slli_epi32(_mm_srli_epi32(f, 28), 16) );
f = _mm_mullo_epi32( _mm_and_si128( f, m ), n );
x = _mm_or_si128( x, _mm_slli_epi32(_mm_srli_epi32(f, 28), 24) );
x = _mm_add_epi8( _mm_shuffle_epi8(x, *(__m128i*)bits.gather), h );
l = __builtin_ctz( ~_mm_movemask_epi8( _mm_cmpeq_epi8( h, x ) ) | (1 << 9) );
x = _mm_shuffle_epi8( x, _mm_add_epi8(*(__m128i*)bits.shift, _mm_set1_epi8(l) ) );
_mm_store_si128( (__m128i*)buffer, x );
return 10 - l;
}
public:
static inline string_type convert(bool neg, unsigned val) {
#ifdef RDTSC
long first_clock = __rdtsc();
#endif
char arena[32];
char* buf = (char*)((uintptr_t)(arena + 16) & ~(uintptr_t)0xf);
*(buf - 1)= '-';
unsigned len = generate(val, buf) + neg;
buf -= neg;
char* end = buf + len;
#ifdef RDTSC
cpu_cycles += __rdtsc() - first_clock;
#endif
return string_type(buf, end);
}
};
string_type itostr(int i) { return Proxy<int>::convert(i < 0, i < 0 ? unsigned(~i) + 1 : i); }
string_type itostr(unsigned i) { return Proxy<unsigned>::convert(false, i); }
unsigned long cycles() { return cpu_cycles; }
void reset() { cpu_cycles = 0; }
}
#endif
}
bool fail(string in, string_type out) {
cout << "failure: " << in << " => " << out << endl;
return false;
}
#define TEST(x, n) \
stringstream ss; \
string_type s = n::itostr(x); \
ss << (long long)x; \
if (::strcmp(ss.str().c_str(), s.c_str())) { \
passed = fail(ss.str(), s); \
break; \
}
#define test(x) { \
passed = true; \
if (0 && passed) { \
char c = CHAR_MIN; \
do { \
TEST(c, x); \
} while (c++ != CHAR_MAX); \
if (!passed) cout << #x << " failed char!!!" << endl; \
} \
if (0 && passed) { \
short c = numeric_limits<short>::min(); \
do { \
TEST(c, x); \
} while (c++ != numeric_limits<short>::max()); \
if (!passed) cout << #x << " failed short!!!" << endl; \
} \
if (passed) { \
int c = numeric_limits<int>::min(); \
do { \
TEST(c, x); \
} while ((c += 100000) < numeric_limits<int>::max() - 100000); \
if (!passed) cout << #x << " failed int!!!" << endl; \
} \
if (passed) { \
unsigned c = numeric_limits<unsigned>::max(); \
do { \
TEST(c, x); \
} while ((c -= 100000) > 100000); \
if (!passed) cout << #x << " failed unsigned int!!!" << endl; \
} \
}
#define time(x, N) \
if (passed) { \
static const int64_t limits[] = \
{0, 10, 100, 1000, 10000, 100000, \
1000000, 10000000, 100000000, 1000000000, 10000000000ULL }; \
long passes = 0; \
cout << #x << ": "; \
progress_timer t; \
uint64_t s = 0; \
if (do_time) { \
for (int n = 0; n < N1; n++) { \
int i = 0; \
while (i < N2) { \
int v = ((NM - i) % limits[N]) | (limits[N] / 10); \
int w = x::itostr(v).size() + \
x::itostr(-v).size(); \
i += w * mult; \
passes++; \
} \
s += i / mult; \
} \
} \
k += s; \
cout << N << " digits: " \
<< s / double(t.elapsed()) * CLOCKS_PER_SEC/1000000 << " MB/sec, " << (x::cycles() / passes >> 1) << " clocks per pass "; \
x::reset(); \
}
#define series(n) \
{ if (do_test) test(n); if (do_time) time(n, 1); if (do_time) time(n, 2); \
if (do_time) time(n, 3); if (do_time) time(n, 4); if (do_time) time(n, 5); \
if (do_time) time(n, 6); if (do_time) time(n, 7); if (do_time) time(n, 8); \
if (do_time) time(n, 9); if (do_time) time(n, 10); }
int N1 = 1, N2 = 500000000, NM = INT_MAX;
int mult = 1; // used to stay under timelimit on ideone
unsigned long long k = 0;
int main(int argc, char** argv) {
bool do_time = 1, do_test = 1;
bool passed = true;
#ifdef HOPMAN_FAST
series(hopman_fast)
#endif
#ifdef WM_VEC
series(wm::vec)
#endif
#ifdef TM_CPP
series(tmn::cpp)
#endif
#ifdef TM_VEC
series(tmn::vec)
#endif
#ifdef AK_UNROLLED
series(ak::unrolled)
#endif
#if defined(AK_BW)
series(ak::bw)
#endif
#if defined(AK_FW)
series(ak::fw)
#endif
return k;
}
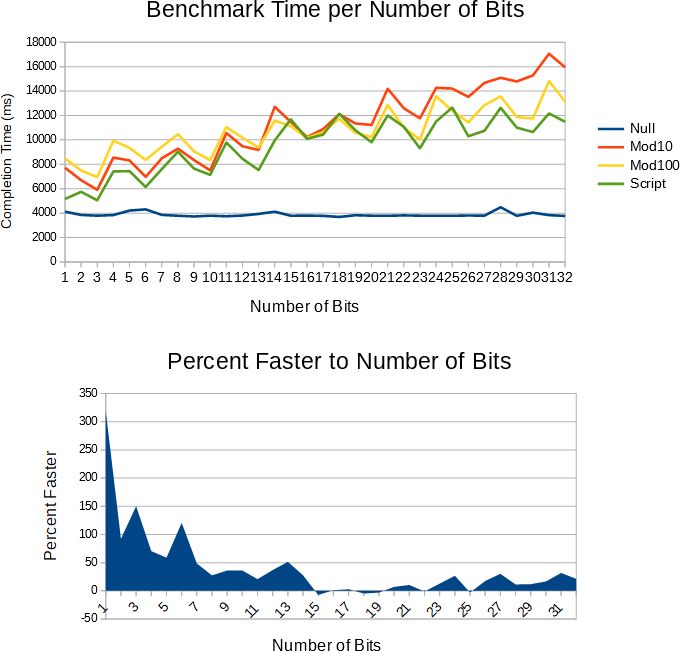
Je pense avoir créé l'algorithme entier-chaîne le plus rapide. Il s'agit d'une variante de l'algorithme Modulo 100 qui est environ 33% plus rapide, et surtout, il est plus rapide pour les petits et les grands nombres. Cela s'appelle l'algorithme Script ItoS. Pour lire l'article qui explique comment j'ai conçu l'algorithme @see https://github.com/kabuki-starship/kabuki-toolkit/wiki/Engineering-a-Faster-Integer-to-String-Algorithm =. Vous pouvez utiliser l'algorithme mais pensez à contribuer à la Kabuki VM et à vérifier Script ; surtout si vous êtes intéressé par AMIL-NLP et/ou les protocoles réseau définis par logiciel.
/** Kabuki Toolkit
@version 0.x
@file ~/source/crabs/print_itos.cc
@author Cale McCollough <[email protected]>
@license Copyright (C) 2017-2018 Cale McCollough <[email protected]>;
All right reserved (R). Licensed under the Apache License, Version
2.0 (the "License"); you may not use this file except in
compliance with the License. You may obtain a copy of the License
[here](http://www.Apache.org/licenses/LICENSE-2.0). Unless
required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or
implied. See the License for the specific language governing
permissions and limitations under the License.
*/
#include <stdafx.h>
#include "print_itos.h"
#if MAJOR_SEAM >= 1 && MINOR_SEAM >= 1
#if MAJOR_SEAM == 1 && MINOR_SEAM == 1
#define DEBUG 1
#define PRINTF(format, ...) printf(format, __VA_ARGS__);
#define PUTCHAR(c) putchar(c);
#define PRINT_PRINTED\
sprintf_s (buffer, 24, "%u", value); *text_end = 0;\
printf ("\n Printed \"%s\" leaving value:\"%s\":%u",\
begin, buffer, (uint)strlen (buffer));
#define PRINT_BINARY PrintBinary (value);
#define PRINT_BINARY_TABLE PrintBinaryTable (value);
#else
#define PRINTF(x, ...)
#define PUTCHAR(c)
#define PRINT_PRINTED
#define PRINT_BINARY
#define PRINT_BINARY_TABLE
#endif
namespace _ {
void PrintLine (char c) {
std::cout << '\n';
for (int i = 80; i > 0; --i)
std::cout << c;
}
char* Print (uint32_t value, char* text, char* text_end) {
// Lookup table for powers of 10.
static const uint32_t k10ToThe[]{
1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000,
1000000000, ~(uint32_t)0 };
/** Lookup table of ASCII char pairs for 00, 01, ..., 99.
To convert this algorithm to big-endian, flip the digit pair bytes. */
static const uint16_t kDigits00To99[100] = {
0x3030, 0x3130, 0x3230, 0x3330, 0x3430, 0x3530, 0x3630, 0x3730, 0x3830,
0x3930, 0x3031, 0x3131, 0x3231, 0x3331, 0x3431, 0x3531, 0x3631, 0x3731,
0x3831, 0x3931, 0x3032, 0x3132, 0x3232, 0x3332, 0x3432, 0x3532, 0x3632,
0x3732, 0x3832, 0x3932, 0x3033, 0x3133, 0x3233, 0x3333, 0x3433, 0x3533,
0x3633, 0x3733, 0x3833, 0x3933, 0x3034, 0x3134, 0x3234, 0x3334, 0x3434,
0x3534, 0x3634, 0x3734, 0x3834, 0x3934, 0x3035, 0x3135, 0x3235, 0x3335,
0x3435, 0x3535, 0x3635, 0x3735, 0x3835, 0x3935, 0x3036, 0x3136, 0x3236,
0x3336, 0x3436, 0x3536, 0x3636, 0x3736, 0x3836, 0x3936, 0x3037, 0x3137,
0x3237, 0x3337, 0x3437, 0x3537, 0x3637, 0x3737, 0x3837, 0x3937, 0x3038,
0x3138, 0x3238, 0x3338, 0x3438, 0x3538, 0x3638, 0x3738, 0x3838, 0x3938,
0x3039, 0x3139, 0x3239, 0x3339, 0x3439, 0x3539, 0x3639, 0x3739, 0x3839,
0x3939, };
static const char kMsbShift[] = { 4, 7, 11, 14, 17, 21, 24, 27, 30, };
if (!text) {
return nullptr;
}
if (text >= text_end) {
return nullptr;
}
uint16_t* text16;
char digit;
uint32_t scalar;
uint16_t digits1and2,
digits3and4,
digits5and6,
digits7and8;
uint32_t comparator;
#if MAJOR_SEAM == 1 && MINOR_SEAM == 1
// Write a bunches of xxxxxx to the buffer for debug purposes.
for (int i = 0; i <= 21; ++i) {
*(text + i) = 'x';
}
*(text + 21) = 0;
char* begin = text;
char buffer[256];
#endif
if (value < 10) {
PRINTF ("\n Range:[0, 9] length:1 ")
if (text + 1 >= text_end) {
return nullptr;
}
*text++ = '0' + (char)value;
PRINT_PRINTED
return text;
}
if (value < 100) {
PRINTF ("\n Range:[10, 99] length:2 ")
if (text + 2 >= text_end) {
return nullptr;
}
*reinterpret_cast<uint16_t*> (text) = kDigits00To99[value];
PRINT_PRINTED
return text + 2;
}
if (value >> 14) {
if (value >> 27) {
if (value >> 30) {
PRINTF ("\n Range:[1073741824, 4294967295] length:10")
Print10:
if (text + 10 >= text_end) {
return nullptr;
}
comparator = 100000000;
digits1and2 = (uint16_t)(value / comparator);
PRINTF ("\n digits1and2:%u", digits1and2)
value -= digits1and2 * comparator;
*reinterpret_cast<uint16_t*> (text) = kDigits00To99[digits1and2];
PRINT_PRINTED
text += 2;
goto Print8;
}
else {
comparator = 1000000000;
if (value >= comparator) {
PRINTF ("\n Range:[100000000, 1073741823] length:10")
goto Print10;
}
PRINTF ("\n Range:[134217727, 999999999] length:9")
if (text + 9 >= text_end) {
return nullptr;
}
comparator = 100000000;
digit = (char)(value / comparator);
*text++ = digit + '0';
PRINT_PRINTED
value -= comparator * digit;
goto Print8;
}
}
else if (value >> 24) {
comparator = k10ToThe[8];
if (value >= comparator) {
PRINTF ("\n Range:[100000000, 134217728] length:9")
if (text + 9 >= text_end) {
return nullptr;
}
*text++ = '1';
PRINT_PRINTED
value -= comparator;
}
PRINTF ("\n Range:[16777216, 9999999] length:8")
if (text + 8 >= text_end) {
return nullptr;
}
Print8:
PRINTF ("\n Print8:")
scalar = 10000;
digits5and6 = (uint16_t)(value / scalar);
digits1and2 = value - scalar * digits5and6;
digits7and8 = digits5and6 / 100;
digits3and4 = digits1and2 / 100;
digits5and6 -= 100 * digits7and8;
digits1and2 -= 100 * digits3and4;
*reinterpret_cast<uint16_t*> (text + 6) =
kDigits00To99[digits1and2];
PRINT_PRINTED
*reinterpret_cast<uint16_t*> (text + 4) =
kDigits00To99[digits3and4];
PRINT_PRINTED
*reinterpret_cast<uint16_t*> (text + 2) =
kDigits00To99[digits5and6];
PRINT_PRINTED
*reinterpret_cast<uint16_t*> (text) =
kDigits00To99[digits7and8];
PRINT_PRINTED
return text + 8;
}
else if (value >> 20) {
comparator = 10000000;
if (value >= comparator) {
PRINTF ("\n Range:[10000000, 16777215] length:8")
if (text + 8 >= text_end) {
return nullptr;
}
*text++ = '1';
PRINT_PRINTED
value -= comparator;
}
else {
PRINTF ("\n Range:[1048576, 9999999] length:7")
if (text + 7 >= text_end) {
return nullptr;
}
}
scalar = 10000;
digits5and6 = (uint16_t)(value / scalar);
digits1and2 = value - scalar * digits5and6;
digits7and8 = digits5and6 / 100;
digits3and4 = digits1and2 / 100;
digits5and6 -= 100 * digits7and8;
digits1and2 -= 100 * digits3and4;;
*reinterpret_cast<uint16_t*> (text + 5) =
kDigits00To99[digits1and2];
PRINT_PRINTED
*reinterpret_cast<uint16_t*> (text + 3) =
kDigits00To99[digits3and4];
PRINT_PRINTED
*reinterpret_cast<uint16_t*> (text + 1) =
kDigits00To99[digits5and6];
PRINT_PRINTED
*text = (char)digits7and8 + '0';
return text + 7;
}
else if (value >> 17) {
comparator = 1000000;
if (value >= comparator) {
PRINTF ("\n Range:[100000, 1048575] length:7")
if (text + 7 >= text_end) {
return nullptr;
}
*text++ = '1';
PRINT_PRINTED
value -= comparator;
}
else {
PRINTF ("\n Range:[131072, 999999] length:6")
if (text + 6 >= text_end) {
return nullptr;
}
}
Print6:
scalar = 10000;
digits5and6 = (uint16_t)(value / scalar);
digits1and2 = value - scalar * digits5and6;
digits7and8 = digits5and6 / 100;
digits3and4 = digits1and2 / 100;
digits5and6 -= 100 * digits7and8;
digits1and2 -= 100 * digits3and4;
text16 = reinterpret_cast<uint16_t*> (text + 6);
*reinterpret_cast<uint16_t*> (text + 4) = kDigits00To99[digits1and2];
PRINT_PRINTED
*reinterpret_cast<uint16_t*> (text + 2) = kDigits00To99[digits3and4];
PRINT_PRINTED
*reinterpret_cast<uint16_t*> (text ) = kDigits00To99[digits5and6];
PRINT_PRINTED
return text + 6;
}
else { // (value >> 14)
if (value >= 100000) {
PRINTF ("\n Range:[65536, 131071] length:6")
goto Print6;
}
PRINTF ("\n Range:[10000, 65535] length:5")
if (text + 5 >= text_end) {
return nullptr;
}
digits5and6 = 10000;
digit = (uint8_t)(value / digits5and6);
value -= digits5and6 * digit;
*text = digit + '0';
PRINT_PRINTED
digits1and2 = (uint16_t)value;
digits5and6 = 100;
digits3and4 = digits1and2 / digits5and6;
digits1and2 -= digits3and4 * digits5and6;
*reinterpret_cast<uint16_t*> (text + 1) =
kDigits00To99[digits3and4];
PRINT_PRINTED
PRINTF ("\n digits1and2:%u", digits1and2)
*reinterpret_cast<uint16_t*> (text + 3) =
kDigits00To99[digits1and2];
PRINT_PRINTED
return text + 5;
}
}
digits1and2 = (uint16_t)value;
if (value >> 10) {
digits5and6 = 10000;
if (digits1and2 >= digits5and6) {
if (text + 5 >= text_end) {
return nullptr;
}
PRINTF ("\n Range:[10000, 16383] length:5")
*text++ = '1';
PRINT_PRINTED
digits1and2 -= digits5and6;
}
else {
PRINTF ("\n Range:[1024, 9999] length:4")
if (text + 4 >= text_end) {
return nullptr;
}
}
digits5and6 = 100;
digits3and4 = digits1and2 / digits5and6;
digits1and2 -= digits3and4 * digits5and6;
*reinterpret_cast<uint16_t*> (text ) = kDigits00To99[digits3and4];
PRINT_PRINTED
*reinterpret_cast<uint16_t*> (text + 2) = kDigits00To99[digits1and2];
PRINT_PRINTED
return text + 4;
}
else {
if (text + 4 >= text_end) {
return nullptr;
}
digits3and4 = 1000;
if (digits1and2 >= digits3and4) {
PRINTF ("\n Range:[1000, 1023] length:4")
digits1and2 -= digits3and4;
text16 = reinterpret_cast<uint16_t*> (text + 2);
*text16-- = kDigits00To99[digits1and2];
PRINT_PRINTED
*text16 = (((uint16_t)'1') | (((uint16_t)'0') << 8));
PRINT_PRINTED
return text + 4;
}
PRINTF ("\n Range:[100, 999] length:3")
digits1and2 = (uint16_t)value;
digits3and4 = 100;
digit = (char)(digits1and2 / digits3and4);
digits1and2 -= digit * digits3and4;
*text = digit + '0';
PRINT_PRINTED
*reinterpret_cast<uint16_t*> (text + 1) = kDigits00To99[digits1and2];
PRINT_PRINTED
return text + 3;
}
}
} //< namespace _
#undef PRINTF
#undef PRINT_PRINTED
#endif //< MAJOR_SEAM >= 1 && MINOR_SEAM >= 1
Auteur
Nous utilisons le code suivant (pour MSVC):
Modèle tBitScanReverse:
#include <intrin.h>
namespace intrin {
#pragma intrinsic(_BitScanReverse)
#pragma intrinsic(_BitScanReverse64)
template<typename TIntegerValue>
__forceinline auto tBitScanReverse(DWORD * out_index, TIntegerValue mask)
-> std::enable_if_t<(std::is_integral<TIntegerValue>::value && sizeof(TIntegerValue) == 4), unsigned char>
{
return _BitScanReverse(out_index, mask);
}
template<typename TIntegerValue>
__forceinline auto tBitScanReverse(DWORD * out_index, TIntegerValue mask)
-> std::enable_if_t<(std::is_integral<TIntegerValue>::value && sizeof(TIntegerValue) == 8), unsigned char>
{
#if !(_M_IA64 || _M_AMD64)
auto res = _BitScanReverse(out_index, (unsigned long)(mask >> 32));
if (res) {
out_index += 32;
return res;
}
return _BitScanReverse(out_index, (unsigned long)mask);
#else
return _BitScanReverse64(out_index, mask);
#endif
}
}
assistants char/wchar_t:
template<typename TChar> inline constexpr TChar ascii_0();
template<> inline constexpr char ascii_0() { return '0'; }
template<> inline constexpr wchar_t ascii_0() { return L'0'; }
template<typename TChar, typename TInt> inline constexpr TChar ascii_DEC(TInt d) { return (TChar)(ascii_0<TChar>() + d); }
Pouvoirs de 10 tables:
static uint32 uint32_powers10[] = {
1,
10,
100,
1000,
10000,
100000,
1000000,
10000000,
100000000,
1000000000
// 123456789
};
static uint64 uint64_powers10[] = {
1ULL,
10ULL,
100ULL,
1000ULL,
10000ULL,
100000ULL,
1000000ULL,
10000000ULL,
100000000ULL,
1000000000ULL,
10000000000ULL,
100000000000ULL,
1000000000000ULL,
10000000000000ULL,
100000000000000ULL,
1000000000000000ULL,
10000000000000000ULL,
100000000000000000ULL,
1000000000000000000ULL,
10000000000000000000ULL
// 1234567890123456789
};
template<typename TUint> inline constexpr const TUint * powers10();
template<> inline constexpr const uint32 * powers10() { return uint32_powers10; }
template<> inline constexpr const uint64 * powers10() { return uint64_powers10; }
Impression réelle:
template<typename TChar, typename TUInt>
__forceinline auto
print_dec(
TUInt u,
TChar * & buffer) -> typename std::enable_if_t<std::is_unsigned<TUInt>::value>
{
if (u < 10) { // 1-digit, including 0
*buffer++ = ascii_DEC<TChar>(u);
}
else {
DWORD log2u;
intrin::tBitScanReverse(&log2u, u); // log2u [3,31] (u >= 10)
DWORD log10u = ((log2u + 1) * 77) >> 8; // log10u [1,9] 77/256 = ln(2) / ln(10)
DWORD digits = log10u + (u >= powers10<TUInt>()[log10u]); // digits [2,10]
buffer += digits;
auto p = buffer;
for (--digits; digits; --digits) {
auto x = u / 10, d = u - x * 10;
*--p = ascii_DEC<TChar>(d);
u = x;
}
*--p = ascii_DEC<TChar>(u);
}
}
La dernière boucle peut être déroulée:
switch (digits) {
case 10: { auto x = u / 10, d = u - x * 10; *--p = ascii_DEC<TChar>(d); u = x; }
case 9: { auto x = u / 10, d = u - x * 10; *--p = ascii_DEC<TChar>(d); u = x; }
case 8: { auto x = u / 10, d = u - x * 10; *--p = ascii_DEC<TChar>(d); u = x; }
case 7: { auto x = u / 10, d = u - x * 10; *--p = ascii_DEC<TChar>(d); u = x; }
case 6: { auto x = u / 10, d = u - x * 10; *--p = ascii_DEC<TChar>(d); u = x; }
case 5: { auto x = u / 10, d = u - x * 10; *--p = ascii_DEC<TChar>(d); u = x; }
case 4: { auto x = u / 10, d = u - x * 10; *--p = ascii_DEC<TChar>(d); u = x; }
case 3: { auto x = u / 10, d = u - x * 10; *--p = ascii_DEC<TChar>(d); u = x; }
case 2: { auto x = u / 10, d = u - x * 10; *--p = ascii_DEC<TChar>(d); u = x; *--p = ascii_DEC<TChar>(u); break; }
default: __assume(0);
}
L'idée principale est la même que @atlaste suggérée auparavant: https://stackoverflow.com/a/29039967/2204001
Je viens de découvrir cela en raison d'une activité récente; Je n'ai pas vraiment le temps d'ajouter des repères, mais je voulais ajouter ce que j'ai écrit par le passé lorsque j'ai besoin d'une conversion rapide d'entier en chaîne ...
https://github.com/CarloWood/ai-utils/blob/master/itoa.h
https://github.com/CarloWood/ai-utils/blob/master/itoa.cxx
L'astuce utilisée ici est que l'utilisateur doit fournir un tableau std :: qui est suffisamment grand (sur sa pile) et que ce code écrit la chaîne dans celui-ci à l'envers, en commençant par les unités, puis en renvoyant un pointeur dans le tableau avec un décalage à l'endroit où le résultat commence réellement.
Par conséquent, cela n'alloue ni ne déplace la mémoire, mais cela nécessite toujours une division et un module par chiffre de résultat (qui je pense être assez rapide car il s'agit simplement de code exécuté en interne sur le CPU; l'accès à la mémoire est généralement le problème à mon humble avis).
Modification de la solution de user434507. Modifié pour utiliser un tableau de caractères au lieu d'une chaîne C++. Fonctionne un peu plus vite. J'ai également déplacé la vérification de 0 plus bas dans le code ... car cela ne se produit jamais pour mon cas particulier. Reculez-le s'il est plus courant pour votre cas.
// Int2Str.cpp : Defines the entry point for the console application.
//
#include <stdio.h>
#include <iostream>
#include "StopWatch.h"
using namespace std;
const char digit_pairs[201] = {
"00010203040506070809"
"10111213141516171819"
"20212223242526272829"
"30313233343536373839"
"40414243444546474849"
"50515253545556575859"
"60616263646566676869"
"70717273747576777879"
"80818283848586878889"
"90919293949596979899"
};
void itostr(int n, char* c) {
int sign = -(n<0);
unsigned int val = (n^sign)-sign;
int size;
if(val>=10000) {
if(val>=10000000) {
if(val>=1000000000) {
size=10;
}
else if(val>=100000000) {
size=9;
}
else size=8;
}
else {
if(val>=1000000) {
size=7;
}
else if(val>=100000) {
size=6;
}
else size=5;
}
}
else {
if(val>=100) {
if(val>=1000) {
size=4;
}
else size=3;
}
else {
if(val>=10) {
size=2;
}
else if(n==0) {
c[0]='0';
c[1] = '\0';
return;
}
else size=1;
}
}
size -= sign;
if(sign)
*c='-';
c += size-1;
while(val>=100) {
int pos = val % 100;
val /= 100;
*(short*)(c-1)=*(short*)(digit_pairs+2*pos);
c-=2;
}
while(val>0) {
*c--='0' + (val % 10);
val /= 10;
}
c[size+1] = '\0';
}
void itostr(unsigned val, char* c)
{
int size;
if(val>=10000)
{
if(val>=10000000)
{
if(val>=1000000000)
size=10;
else if(val>=100000000)
size=9;
else
size=8;
}
else
{
if(val>=1000000)
size=7;
else if(val>=100000)
size=6;
else
size=5;
}
}
else
{
if(val>=100)
{
if(val>=1000)
size=4;
else
size=3;
}
else
{
if(val>=10)
size=2;
else if (val==0) {
c[0]='0';
c[1] = '\0';
return;
}
else
size=1;
}
}
c += size-1;
while(val>=100)
{
int pos = val % 100;
val /= 100;
*(short*)(c-1)=*(short*)(digit_pairs+2*pos);
c-=2;
}
while(val>0)
{
*c--='0' + (val % 10);
val /= 10;
}
c[size+1] = '\0';
}
void test() {
bool foundmismatch = false;
char str[16];
char compare[16];
for(int i = -1000000; i < 1000000; i++) {
int random = Rand();
itostr(random, str);
itoa(random, compare, 10);
if(strcmp(str, compare) != 0) {
cout << "Mismatch found: " << endl;
cout << "Generated: " << str << endl;
cout << "Reference: " << compare << endl;
foundmismatch = true;
}
}
if(!foundmismatch) {
cout << "No mismatch found!" << endl;
}
cin.get();
}
void benchmark() {
StopWatch stopwatch;
stopwatch.setup("Timer");
stopwatch.reset();
stopwatch.start();
char str[16];
for(unsigned int i = 0; i < 2000000; i++) {
itostr(i, str);
}
stopwatch.stop();
cin.get();
}
int main( int argc, const char* argv[]) {
benchmark();
}