Testez si un nombre est fibonacci
Je sais comment faire la liste des nombres de Fibonacci, mais je ne sais pas comment puis-je tester si un nombre donné appartient à la liste des fibonacci - une façon qui vient à l'esprit est de générer la liste des fib. nombres jusqu'à ce nombre et voir s'il appartient au tableau, mais il doit y avoir une autre méthode, plus simple et plus rapide.
Des idées ?
Un test très agréable est que N est un nombre de Fibonacci si et seulement si 5 N^2 + 4 ou 5N^2 – 4 est un nombre carré. Pour des idées sur la façon de tester efficacement qu'un nombre est carré, reportez-vous à discussion SO .
J'espère que cela t'aides
Un entier positif ω est un nombre de Fibonacci si et seulement si l'un de 5ω2 + 4 et 5ω2 - 4 est un carré parfait.
Voir The Faboulous Fibonacci Numbers pour en savoir plus.

#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
echo "$victim is a fibonacci number"
else
echo "$victim aint"
fi
Si vos nombres sont de taille limitée, simplement mettre tous les nombres de fibonacci sous la limite supérieure dans une table de hachage et tester le confinement fera l'affaire. Il y a très peu de nombres de fibonacci (par exemple, seulement 38 en dessous de 5 mln), car ils se développent de façon exponentielle.
Si vos nombres sont pas de taille limitée, alors l'astuce suggérée avec le test carré sera presque sûrement plus lente que de générer la séquence de fibonacci jusqu'à ce que le nombre soit trouvé ou dépassé.
Vers une solution, jetez un œil à la formule de Binet.
(Recherchez "Expression en forme fermée" sous Numéro de Fibonacci sur Wikipedia)
Il dit que la séquence des nombres de Fibonacci est créée par une simple formule fermée:
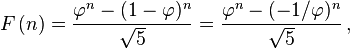
Je crois que si vous résolvez pour n et testez si n est un entier, vous aurez votre réponse.
Modifier Comme le souligne @psmears, le même article Wikipédia contient également une section sur la détection des numéros de Fibonacci. Wikipédia est une excellente source.
Un entier positif ω est un nombre de Fibonacci
Si et seulement si l'un des 5ω2 + 4 et 5ω2 - 4 est un carré parfait
from Les (fabuleux) numéros FIBONACCI d'Alfred Posamentier et Ingmar Lehmann
bool isFibonacci(int w)
{
double X1 = 5 * Math.Pow(w, 2) + 4;
double X2 = 5 * Math.Pow(w, 2) - 4;
long X1_sqrt = (long)Math.Sqrt(X1);
long X2_sqrt = (long)Math.Sqrt(X2);
return (X1_sqrt*X1_sqrt == X1) || (X2_sqrt*X2_sqrt == X2) ;
}
Je l'ai copié à partir de cette source
Extrait qui imprime les nombres de Fibonacci entre 1k et 10k.
for (int i = 1000; i < 10000; i++)
{
if (isFibonacci(i))
Console.Write(" "+i);
}
OMG Il n'y a que QUATRE !!!
Avec une autre méthode
from math import *
phi = 1.61803399
sqrt5 = sqrt(5)
def F(n):
return int((phi**n - (1-phi)**n) /sqrt5)
def isFibonacci(z):
return F(int(floor(log(sqrt5*z,phi)+0.5))) == z
print [i for i in range(1000,10000) if isFibonacci(i)]
Voir la section "Reconnaître les numéros de Fibonacci" sur le article wikipedia sur les numéros de Fibonacci .
Étant donné que les nombres de Fibonacci augmentent de façon exponentielle, la méthode que vous proposez est assez rapide. Un autre est this .
Sur la base des réponses précédentes de moi et de psmears, j'ai écrit ce code C #.
Il passe lentement par les étapes et peut clairement être réduit et optimisé:
// Input: T: number to test.
// Output: idx: index of the number in the Fibonacci sequence.
// eg: idx for 8 is 6. (0, 1, 1, 2, 3, 5, 8)
// Return value: True if Fibonacci, False otherwise.
static bool IsFib(long T, out int idx)
{
double root5 = Math.Sqrt(5);
double PSI = (1 + root5) / 2;
// For reference, IsFib(72723460248141) should show it is the 68th Fibonacci number
double a;
a = T*root5;
a = Math.Log(a) / Math.Log(PSI);
a += 0.5;
a = Math.Floor(a);
idx = (Int32)a;
long u = (long)Math.Floor(Math.Pow(PSI, a)/root5 + 0.5);
if (u == T)
{
return true;
}
else
{
idx = 0;
return false;
}
}
Les tests révèlent que cela fonctionne pour les 69 premiers numéros de Fibonacci, mais tombe en panne pour le 70e.
F(69) = 117,669,030,460,994 - Works
F(70) = 190,392,490,709,135 - Fails
Dans l'ensemble, à moins que vous n'utilisiez une bibliothèque BigInt d'une certaine sorte, il est probablement préférable d'avoir une simple table de recherche des numéros de Fibonacci et de vérifier cela, plutôt que d'exécuter un algorithme.
Une liste des 300 premiers numéros est facilement accessible en ligne.
Mais ce code décrit un algorithme réalisable, à condition que vous ayez suffisamment de précision et que vous ne débordiez pas votre système de représentation numérique.
Re: le code d'Ahmad - une approche plus simple sans récursivité ni pointeurs, assez naïf, mais ne nécessite pratiquement aucune puissance de calcul pour quoi que ce soit à court de nombres vraiment titanesques (environ 2N ajouts pour vérifier le nombre Nth fib, qui sur une machine moderne prendra des millisecondes au pire)
// renvoie pos s'il trouve quelque chose, 0 s'il ne le fait pas (C/C++ traite toute valeur! = 0 comme vraie, donc même résultat final)
int isFib (long n)
{
int pos = 2;
long last = 1;
long current = 1;
long temp;
while (current < n)
{
temp = last;
last = current;
current = current + temp;
pos++;
}
if (current == n)
return pos;
else
return 0;
}
De Wikipedia: http://en.wikipedia.org/wiki/Fibonacci_number
Un entier positif z est un nombre de Fibonacci si et seulement si l'un de 5z ^ 2 + 4 ou 5z ^ 2 - 4 est un carré parfait.
L'expression générale d'un nombre de Fibonacci est F(n) = [[(1 + sqrt (5))/2] sup n + 1 - [(1-sqrt (5))/2] sup n + 1]/sqrt (5) ..... (*) La deuxième exponentielle va à zéro pour les grands n et effectuant les opérations numériques que nous obtenons F(n) = [(1,618) sup n + 1]/2,236
Si K est le nombre à tester, log (k * 2.2336)/log (1.618) doit être un entier!
Exemple pour K égal à 13 ma calculatrice donne la réponse 7.00246 Pour K égal à 14 la réponse est 7.1564.
Vous pouvez augmenter la confiance dans le résultat en prenant l'entier le plus proche de la réponse et le remplacer par (*) pour confirmer que le résultat est K
J'ai effectué des tests de performances sur les méthodes présentées ici avec un simple ajout, le pré-calcul d'un tableau et la mémorisation des résultats dans un hachage. Pour Perl, au moins, la méthode de la quadrature est un peu plus rapide que la méthode logarithmique, peut-être 20% plus rapide. Comme le souligne Abelenky, c'est un compromis entre si vous avez la place pour la mise au carré des nombres de bits.
Certes, le moyen le plus rapide est de hacher tous les numéros de Fibonacci dans votre espace de domaine. Le long d'un autre point qu'abelenky fait, il n'y a que 94 de ces rejets qui sont moins de 2 ^ 64.
Vous devez simplement les pré-calculer et les mettre dans un hachage Perl, Python, ou autre).
Les propriétés des nombres de Fibonacci sont très intéressantes, mais les utiliser pour déterminer si un entier dans un programme informatique en est un est un peu comme écrire un sous-programme pour calculer pi à chaque démarrage du programme.
Ceci est ma solution, je ne sais pas si elle référence. J'espère que ça aide!
def is_fibonacci?(i)
a,b=0,1
until b >= i
a,b=b,a+b
return true if b == i
end
end
ce que a, b = b, a + b fait
0, 1 = 1, 0 +1
1, 1 = 1, 1 + 1
1, 2 = 2, 1 + 2
2, 3 = 3, 2 + 3
fib1 = fib2
fib2 = fib1 + fib2
A Scala version-
def isFib(n: Int): Boolean = {
def checkFib(f1: Int = 1, f2: Int = 1): Boolean = {
if(n == f1 || n == f2) true
else if(n < f2) false
else checkFib(f2, f1+f2)
}
checkFib()
}
Quelle est la taille des chiffres avec lesquels vous traitez?
Une table de recherche pourrait-elle fonctionner pour vous? (une liste pré-calculée de nombres dans lesquels vous pouvez rechercher)
Il y a aussi une expression de forme fermée que je suppose que vous pourriez inverser pour obtenir la réponse analytiquement (bien que je ne sois pas mathématicien, je ne peux donc pas promettre que cette suggestion a du sens)
La solution Java peut être effectuée comme ci-dessous. Mais il peut encore être optimisé
La solution suivante fonctionne pour
- 1≤T≤10 ^ 5
- 1≤N≤10 ^ 10
T est le nombre de cas de test, N est la plage de nombres
import Java.util.Scanner;
import Java.math.BigDecimal;
import Java.math.RoundingMode;
public class FibonacciTester {
private static BigDecimal zero = BigDecimal.valueOf(0);
private static BigDecimal one = BigDecimal.valueOf(1);
private static BigDecimal two = BigDecimal.valueOf(2);
private static BigDecimal four = BigDecimal.valueOf(4);
private static BigDecimal five = BigDecimal.valueOf(5);
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
BigDecimal[] inputs = new BigDecimal[n];
for (int i = 0; i < n; i++) {
inputs[i] = sc.nextBigDecimal();
}
for (int i = 0; i < inputs.length; i++) {
if (isFibonacci(inputs[i]))
System.out.println("IsFibo");
else
System.out.println("IsNotFibo");
}
}
public static boolean isFibonacci(BigDecimal num) {
if (num.compareTo(zero) <= 0) {
return false;
}
BigDecimal base = num.multiply(num).multiply(five);
BigDecimal possibility1 = base.add(four);
BigDecimal possibility2 = base.subtract(four);
return (isPerfectSquare(possibility1) || isPerfectSquare(possibility2));
}
public static boolean isPerfectSquare(BigDecimal num) {
BigDecimal squareRoot = one;
BigDecimal square = one;
BigDecimal i = one;
BigDecimal newSquareRoot;
int comparison = -1;
while (comparison != 0) {
if (comparison < 0) {
i = i.multiply(two);
newSquareRoot = squareRoot.add(i).setScale(0, RoundingMode.HALF_UP);
} else {
i = i.divide(two);
newSquareRoot = squareRoot.subtract(i).setScale(0, RoundingMode.HALF_UP);
}
if (newSquareRoot.compareTo(squareRoot) == 0) {
return false;
}
squareRoot = newSquareRoot;
square = squareRoot.multiply(squareRoot);
comparison = square.compareTo(num);
}
return true;
}
}