Comment trouver une factorielle?
Comment puis-je écrire un programme pour trouver la factorielle d'un nombre naturel?
Cela fonctionnera pour le factoriel (bien qu’un très petit sous-ensemble) d’entiers positifs:
unsigned long factorial(unsigned long f)
{
if ( f == 0 )
return 1;
return(f * factorial(f - 1));
}
printf("%i", factorial(5));
En raison de la nature de votre problème (et du niveau que vous avez admis), cette solution repose davantage sur le concept de résolution de ce problème que sur une fonction qui sera utilisée dans le prochain "Moteur de permutation".
Ceci calcule les factorielles d'entiers non négatifs [*] jusqu'à ULONG_MAX, qui auront tellement de chiffres qu'il est peu probable que votre machine puisse stocker beaucoup plus, même si elle a le temps de les calculer. Utilise la bibliothèque GNU multi-précision, avec laquelle vous devez créer un lien.
#include <assert.h>
#include <stdio.h>
#include <stdlib.h>
#include <gmp.h>
void factorial(mpz_t result, unsigned long input) {
mpz_set_ui(result, 1);
while (input > 1) {
mpz_mul_ui(result, result, input--);
}
}
int main() {
mpz_t fact;
unsigned long input = 0;
char *buf;
mpz_init(fact);
scanf("%lu", &input);
factorial(fact, input);
buf = malloc(mpz_sizeinbase(fact, 10) + 1);
assert(buf);
mpz_get_str(buf, 10, fact);
printf("%s\n", buf);
free(buf);
mpz_clear(fact);
}
Exemple de sortie:
$ make factorial CFLAGS="-L/bin/ -lcyggmp-3 -pedantic" -B && ./factorial
cc -L/bin/ -lcyggmp-3 -pedantic factorial.c -o factorial
100
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
[*] Si vous voulez dire autre chose par "numéro", vous devrez être plus précis. Je ne connais aucun autre nombre pour lequel la factorielle est définie, malgré les vaillants efforts de Pascal pour étendre le domaine en utilisant la fonction Gamma.
Pourquoi le faire en C quand vous pouvez le faire en Haskell :
Étudiant de première année Haskell
fac n = if n == 0
then 1
else n * fac (n-1)
Sophomore Haskell, programmeur au MIT (A étudié Scheme à titre d'étudiant de première année)
fac = (\(n) ->
(if ((==) n 0)
then 1
else ((*) n (fac ((-) n 1)))))
Programmeur Junior Haskell (Joueur débutant de Peano)
fac 0 = 1
fac (n+1) = (n+1) * fac n
Un autre programmeur junior de Haskell (Lire que les motifs n + k sont «une partie dégoûtante de Haskell» 1 Et ont rejoint le mouvement «Ban n + k motifs» [2])
fac 0 = 1
fac n = n * fac (n-1)
Senior programmeur Haskell (A voté pour Nixon Buchanan Bush - "se penche à droite")
fac n = foldr (*) 1 [1..n]
Un autre programmeur expérimenté de Haskell .__ (vota pour McGovern Biafra Nader - «penche à gauche»)
fac n = foldl (*) 1 [1..n]
Encore un autre programmeur senior de Haskell (Penché tellement à droite qu’il revint encore à gauche!)
-- using foldr to simulate foldl
fac n = foldr (\x g n -> g (x*n)) id [1..n] 1
Mémo du programmeur Haskell (Prend Ginkgo Biloba tous les jours)
facs = scanl (*) 1 [1..]
fac n = facs !! n
Pointless (ahem) Programmeur Haskell «sans points» (Étudié à Oxford)
fac = foldr (*) 1 . enumFromTo 1
Programmeur itératif Haskell (Ancien programmeur Pascal)
fac n = result (for init next done)
where init = (0,1)
next (i,m) = (i+1, m * (i+1))
done (i,_) = i==n
result (_,m) = m
for i n d = until d n i
Programmeur Haskell à une ligne itératif (Ancien programmeur APL et C)
fac n = snd (until ((>n) . fst) (\(i,m) -> (i+1, i*m)) (1,1))
Programmateur accumulateur Haskell (Atteignant un point culminant rapide)
facAcc a 0 = a
facAcc a n = facAcc (n*a) (n-1)
fac = facAcc 1
Programmeur Haskell de passage à la suite (Il a élevé des lapins dans les premières années, puis a déménagé dans le New Jersey)
facCps k 0 = k 1
facCps k n = facCps (k . (n *)) (n-1)
fac = facCps id
Programmeur de Boy Scout Haskell (Aime faire des nœuds; il est toujours "respectueux", il Appartient à l'Église du Point le moins fixe [8])
y f = f (y f)
fac = y (\f n -> if (n==0) then 1 else n * f (n-1))
Programmeur combinatoire Haskell (Évite les variables, sinon l’obscurcissement; Tout ce currying n’est qu’une phase, bien qu’il gêne rarement)
s f g x = f x (g x)
k x y = x
b f g x = f (g x)
c f g x = f x g
y f = f (y f)
cond p f g x = if p x then f x else g x
fac = y (b (cond ((==) 0) (k 1)) (b (s (*)) (c b pred)))
Programmeur Haskell à codage de liste .__ (préfère compter en unaire)
arb = () -- "undefined" is also a good RHS, as is "arb" :)
listenc n = replicate n arb
listprj f = length . f . listenc
listprod xs ys = [ i (x,y) | x<-xs, y<-ys ]
where i _ = arb
facl [] = listenc 1
facl n@(_:pred) = listprod n (facl pred)
fac = listprj facl
Programmeur d'interprétation Haskell (Jamais "rencontré une langue" qu'il n'a pas aimé)
-- a dynamically-typed term language
data Term = Occ Var
| Use Prim
| Lit Integer
| App Term Term
| Abs Var Term
| Rec Var Term
type Var = String
type Prim = String
-- a domain of values, including functions
data Value = Num Integer
| Bool Bool
| Fun (Value -> Value)
instance Show Value where
show (Num n) = show n
show (Bool b) = show b
show (Fun _) = ""
prjFun (Fun f) = f
prjFun _ = error "bad function value"
prjNum (Num n) = n
prjNum _ = error "bad numeric value"
prjBool (Bool b) = b
prjBool _ = error "bad boolean value"
binOp inj f = Fun (\i -> (Fun (\j -> inj (f (prjNum i) (prjNum j)))))
-- environments mapping variables to values
type Env = [(Var, Value)]
getval x env = case lookup x env of
Just v -> v
Nothing -> error ("no value for " ++ x)
-- an environment-based evaluation function
eval env (Occ x) = getval x env
eval env (Use c) = getval c prims
eval env (Lit k) = Num k
eval env (App m n) = prjFun (eval env m) (eval env n)
eval env (Abs x m) = Fun (\v -> eval ((x,v) : env) m)
eval env (Rec x m) = f where f = eval ((x,f) : env) m
-- a (fixed) "environment" of language primitives
times = binOp Num (*)
minus = binOp Num (-)
equal = binOp Bool (==)
cond = Fun (\b -> Fun (\x -> Fun (\y -> if (prjBool b) then x else y)))
prims = [ ("*", times), ("-", minus), ("==", equal), ("if", cond) ]
-- a term representing factorial and a "wrapper" for evaluation
facTerm = Rec "f" (Abs "n"
(App (App (App (Use "if")
(App (App (Use "==") (Occ "n")) (Lit 0))) (Lit 1))
(App (App (Use "*") (Occ "n"))
(App (Occ "f")
(App (App (Use "-") (Occ "n")) (Lit 1))))))
fac n = prjNum (eval [] (App facTerm (Lit n)))
Static Haskell Programmer (Il le fait avec classe, il a ce fundep Jones! Après "Le plaisir avec les dépendances fonctionnelles" de Thomas Hallgren [7])
-- static Peano constructors and numerals
data Zero
data Succ n
type One = Succ Zero
type Two = Succ One
type Three = Succ Two
type Four = Succ Three
-- dynamic representatives for static Peanos
zero = undefined :: Zero
one = undefined :: One
two = undefined :: Two
three = undefined :: Three
four = undefined :: Four
-- addition, a la Prolog
class Add a b c | a b -> c where
add :: a -> b -> c
instance Add Zero b b
instance Add a b c => Add (Succ a) b (Succ c)
-- multiplication, a la Prolog
class Mul a b c | a b -> c where
mul :: a -> b -> c
instance Mul Zero b Zero
instance (Mul a b c, Add b c d) => Mul (Succ a) b d
-- factorial, a la Prolog
class Fac a b | a -> b where
fac :: a -> b
instance Fac Zero One
instance (Fac n k, Mul (Succ n) k m) => Fac (Succ n) m
-- try, for "instance" (sorry):
--
-- :t fac four
Programmeur débutant de Haskell pour les études supérieures (L’enseignement supérieur tend à libérer les préoccupations insignifiantes Concernant, par exemple, l’efficacité des nombres entiers basés sur le matériel)
-- the natural numbers, a la Peano
data Nat = Zero | Succ Nat
-- iteration and some applications
iter z s Zero = z
iter z s (Succ n) = s (iter z s n)
plus n = iter n Succ
mult n = iter Zero (plus n)
-- primitive recursion
primrec z s Zero = z
primrec z s (Succ n) = s n (primrec z s n)
-- two versions of factorial
fac = snd . iter (one, one) (\(a,b) -> (Succ a, mult a b))
fac' = primrec one (mult . Succ)
-- for convenience and testing (try e.g. "fac five")
int = iter 0 (1+)
instance Show Nat where
show = show . int
(zero : one : two : three : four : five : _) = iterate Succ Zero
Origamist Haskell programmer
(always starts out with the “basic Bird fold”)
-- (curried, list) fold and an application
fold c n [] = n
fold c n (x:xs) = c x (fold c n xs)
prod = fold (*) 1
-- (curried, boolean-based, list) unfold and an application
unfold p f g x =
if p x
then []
else f x : unfold p f g (g x)
downfrom = unfold (==0) id pred
-- hylomorphisms, as-is or "unfolded" (ouch! sorry ...)
refold c n p f g = fold c n . unfold p f g
refold' c n p f g x =
if p x
then n
else c (f x) (refold' c n p f g (g x))
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = refold (*) 1 (==0) id pred
fac'' = refold' (*) 1 (==0) id pred
Programmeur Haskell à tendance cartésienne (Préfère la cuisine grecque, évite les épices indiennes épicées; Inspiré de «Sorting Morphisms» de Lex Augusteijn [3])
-- (product-based, list) catamorphisms and an application
cata (n,c) [] = n
cata (n,c) (x:xs) = c (x, cata (n,c) xs)
mult = uncurry (*)
prod = cata (1, mult)
-- (co-product-based, list) anamorphisms and an application
ana f = either (const []) (cons . pair (id, ana f)) . f
cons = uncurry (:)
downfrom = ana uncount
uncount 0 = Left ()
uncount n = Right (n, n-1)
-- two variations on list hylomorphisms
hylo f g = cata g . ana f
hylo' f (n,c) = either (const n) (c . pair (id, hylo' f (c,n))) . f
pair (f,g) (x,y) = (f x, g y)
-- several versions of factorial, all (extensionally) equivalent
fac = prod . downfrom
fac' = hylo uncount (1, mult)
fac'' = hylo' uncount (1, mult)
Doctorat Programmeur Haskell (A mangé tellement de bananes que ses yeux se sont troublés, maintenant il a besoin de nouvelles lentilles!)
-- explicit type recursion based on functors
newtype Mu f = Mu (f (Mu f)) deriving Show
in x = Mu x
out (Mu x) = x
-- cata- and ana-morphisms, now for *arbitrary* (regular) base functors
cata phi = phi . fmap (cata phi) . out
ana psi = in . fmap (ana psi) . psi
-- base functor and data type for natural numbers,
-- using a curried elimination operator
data N b = Zero | Succ b deriving Show
instance Functor N where
fmap f = nelim Zero (Succ . f)
nelim z s Zero = z
nelim z s (Succ n) = s n
type Nat = Mu N
-- conversion to internal numbers, conveniences and applications
int = cata (nelim 0 (1+))
instance Show Nat where
show = show . int
zero = in Zero
suck = in . Succ -- pardon my "French" (Prelude conflict)
plus n = cata (nelim n suck )
mult n = cata (nelim zero (plus n))
-- base functor and data type for lists
data L a b = Nil | Cons a b deriving Show
instance Functor (L a) where
fmap f = lelim Nil (\a b -> Cons a (f b))
lelim n c Nil = n
lelim n c (Cons a b) = c a b
type List a = Mu (L a)
-- conversion to internal lists, conveniences and applications
list = cata (lelim [] (:))
instance Show a => Show (List a) where
show = show . list
prod = cata (lelim (suck zero) mult)
upto = ana (nelim Nil (diag (Cons . suck)) . out)
diag f x = f x x
fac = prod . upto
Post-doc Haskell programmer
(from Uustalu, Vene and Pardo’s “Recursion Schemes from Comonads” [4])
-- explicit type recursion with functors and catamorphisms
newtype Mu f = In (f (Mu f))
unIn (In x) = x
cata phi = phi . fmap (cata phi) . unIn
-- base functor and data type for natural numbers,
-- using locally-defined "eliminators"
data N c = Z | S c
instance Functor N where
fmap g Z = Z
fmap g (S x) = S (g x)
type Nat = Mu N
zero = In Z
suck n = In (S n)
add m = cata phi where
phi Z = m
phi (S f) = suck f
mult m = cata phi where
phi Z = zero
phi (S f) = add m f
-- explicit products and their functorial action
data Prod e c = Pair c e
outl (Pair x y) = x
outr (Pair x y) = y
fork f g x = Pair (f x) (g x)
instance Functor (Prod e) where
fmap g = fork (g . outl) outr
-- comonads, the categorical "opposite" of monads
class Functor n => Comonad n where
extr :: n a -> a
dupl :: n a -> n (n a)
instance Comonad (Prod e) where
extr = outl
dupl = fork id outr
-- generalized catamorphisms, zygomorphisms and paramorphisms
gcata :: (Functor f, Comonad n) =>
(forall a. f (n a) -> n (f a))
-> (f (n c) -> c) -> Mu f -> c
gcata dist phi = extr . cata (fmap phi . dist . fmap dupl)
zygo chi = gcata (fork (fmap outl) (chi . fmap outr))
para :: Functor f => (f (Prod (Mu f) c) -> c) -> Mu f -> c
para = zygo In
-- factorial, the *hard* way!
fac = para phi where
phi Z = suck zero
phi (S (Pair f n)) = mult f (suck n)
-- for convenience and testing
int = cata phi where
phi Z = 0
phi (S f) = 1 + f
instance Show (Mu N) where
show = show . int
Professeur titulaire (Enseignement de Haskell aux étudiants de première année)
fac n = product [1..n]
Grâce à Christoph, une solution C99 qui fonctionne pour pas mal de "nombres":
#include <math.h>
#include <stdio.h>
double fact(double x)
{
return tgamma(x+1.);
}
int main()
{
printf("%f %f\n", fact(3.0), fact(5.0));
return 0;
}
produit 6.000000 120.000000
Pour n grand, vous pouvez rencontrer quelques problèmes et vous pouvez utiliser l'approximation de Stirling:
Lequel est:
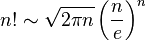
Si votre objectif principal est une fonction de recherche intéressante:
int facorial(int a) {
int b = 1, c, d, e;
a--;
for (c = a; c > 0; c--)
for (d = b; d > 0; d--)
for (e = c; e > 0; e--)
b++;
return b;
}
(Non recommandé comme algorithme pour une utilisation réelle.)
En C99 (ou Java), j'écrirais la fonction factorielle de manière itérative comme ceci:
int factorial(int n)
{
int result = 1;
for (int i = 2; i <= n; i++)
{
result *= i;
}
return result;
}
C n’est pas un langage fonctionnel et vous ne pouvez pas vous fier à l’optimisation des appels ultérieurs. Donc, n'utilisez pas la récursivité en C (ou Java) à moins que vous n'en ayez besoin.
Le fait que factorial soit souvent utilisé comme premier exemple de récursivité ne signifie pas nécessairement que vous avez besoin de récursivité pour le calculer.
Cela débordera silencieusement si n est trop grand, comme c'est le cas dans C (et Java).
Si les nombres que int peut représenter sont trop petits pour les factorielles que vous voulez calculer, choisissez un autre type de nombre. long long s'il doit être légèrement plus grand, float ou double si n n'est pas trop grand et que l'imprécision ne vous gêne pas, ou de grands entiers si vous voulez les valeurs exactes de facteurs très grands.
une version queue-récursive:
long factorial(long n)
{
return tr_fact(n, 1);
}
static long tr_fact(long n, long result)
{
if(n==1)
return result;
else
return tr_fact(n-1, n*result);
}
Voici un programme C qui utilise l'implémentation BIGNUM d'OPENSSL et qui, par conséquent, n'est pas particulièrement utile pour les étudiants. (Bien sûr, accepter un BIGNUM comme paramètre d'entrée est fou, mais il est utile pour démontrer l'interaction entre les BIGNUM).
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <openssl/crypto.h>
#include <openssl/bn.h>
BIGNUM *factorial(const BIGNUM *num)
{
BIGNUM *count = BN_new();
BIGNUM *fact = NULL;
BN_CTX *ctx = NULL;
BN_one(count);
if( BN_cmp(num, BN_value_one()) <= 0 )
{
return count;
}
ctx = BN_CTX_new();
fact = BN_dup(num);
BN_sub(count, fact, BN_value_one());
while( BN_cmp(count, BN_value_one()) > 0 )
{
BN_mul(fact, count, fact, ctx);
BN_sub(count, count, BN_value_one());
}
BN_CTX_free(ctx);
BN_free(count);
return fact;
}
Ce programme de test montre comment créer un nombre à saisir et comment utiliser la valeur de retour:
int main(int argc, char *argv[])
{
const char *test_cases[] =
{
"0", "1",
"1", "1",
"4", "24",
"15", "1307674368000",
"30", "265252859812191058636308480000000",
"56", "710998587804863451854045647463724949736497978881168458687447040000000000000",
NULL, NULL
};
int index = 0;
BIGNUM *bn = NULL;
BIGNUM *fact = NULL;
char *result_str = NULL;
for( index = 0; test_cases[index] != NULL; index += 2 )
{
BN_dec2bn(&bn, test_cases[index]);
fact = factorial(bn);
result_str = BN_bn2dec(fact);
printf("%3s: %s\n", test_cases[index], result_str);
assert(strcmp(result_str, test_cases[index + 1]) == 0);
OPENSSL_free(result_str);
BN_free(fact);
BN_free(bn);
bn = NULL;
}
return 0;
}
Compilé avec gcc:
gcc factorial.c -o factorial -g -lcrypto
int factorial(int n){
return n <= 1 ? 1 : n * factorial(n-1);
}
#Newbie programmer
def factorial(x):
if x == 0:
return 1
else:
return x * factorial(x - 1)
print factorial(6)
#First year programmer, studied Pascal
def factorial(x):
result = 1
i = 2
while i <= x:
result = result * i
i = i + 1
return result
print factorial(6)
#First year programmer, studied C
def fact(x): #{
result = i = 1;
while (i <= x): #{
result *= i;
i += 1;
#}
return result;
#}
print(fact(6))
#First year programmer, SICP
@tailcall
def fact(x, acc=1):
if (x > 1): return (fact((x - 1), (acc * x)))
else: return acc
print(fact(6))
#First year programmer, Python
def Factorial(x):
res = 1
for i in xrange(2, x + 1):
res *= i
return res
print Factorial(6)
#Lazy Python programmer
def fact(x):
return x > 1 and x * fact(x - 1) or 1
print fact(6)
#Lazier Python programmer
f = lambda x: x and x * f(x - 1) or 1
print f(6)
#Python expert programmer
import operator as op
import functional as f
fact = lambda x: f.foldl(op.mul, 1, xrange(2, x + 1))
print fact(6)
#Python hacker
import sys
@tailcall
def fact(x, acc=1):
if x: return fact(x.__sub__(1), acc.__mul__(x))
return acc
sys.stdout.write(str(fact(6)) + '\n')
#EXPERT PROGRAMMER
import c_math
fact = c_math.fact
print fact(6)
#ENGLISH EXPERT PROGRAMMER
import c_maths
fact = c_maths.fact
print fact(6)
#Web designer
def factorial(x):
#-------------------------------------------------
#--- Code snippet from The Math Vault ---
#--- Calculate factorial (C) Arthur Smith 1999 ---
#-------------------------------------------------
result = str(1)
i = 1 #Thanks Adam
while i <= x:
#result = result * i #It's faster to use *=
#result = str(result * result + i)
#result = int(result *= i) #??????
result str(int(result) * i)
#result = int(str(result) * i)
i = i + 1
return result
print factorial(6)
#Unix programmer
import os
def fact(x):
os.system('factorial ' + str(x))
fact(6)
#Windows programmer
NULL = None
def CalculateAndPrintFactorialEx(dwNumber,
hOutputDevice,
lpLparam,
lpWparam,
lpsscSecurity,
*dwReserved):
if lpsscSecurity != NULL:
return NULL #Not implemented
dwResult = dwCounter = 1
while dwCounter <= dwNumber:
dwResult *= dwCounter
dwCounter += 1
hOutputDevice.write(str(dwResult))
hOutputDevice.write('\n')
return 1
import sys
CalculateAndPrintFactorialEx(6, sys.stdout, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL, NULL)
#Enterprise programmer
def new(cls, *args, **kwargs):
return cls(*args, **kwargs)
class Number(object):
pass
class IntegralNumber(int, Number):
def toInt(self):
return new (int, self)
class InternalBase(object):
def __init__(self, base):
self.base = base.toInt()
def getBase(self):
return new (IntegralNumber, self.base)
class MathematicsSystem(object):
def __init__(self, ibase):
Abstract
@classmethod
def getInstance(cls, ibase):
try:
cls.__instance
except AttributeError:
cls.__instance = new (cls, ibase)
return cls.__instance
class StandardMathematicsSystem(MathematicsSystem):
def __init__(self, ibase):
if ibase.getBase() != new (IntegralNumber, 2):
raise NotImplementedError
self.base = ibase.getBase()
def calculateFactorial(self, target):
result = new (IntegralNumber, 1)
i = new (IntegralNumber, 2)
while i <= target:
result = result * i
i = i + new (IntegralNumber, 1)
return result
print StandardMathematicsSystem.getInstance(new (InternalBase, new (IntegralNumber, 2))).calculateFactorial(new (IntegralNumber, 6))
source http://Gist.github.com/25049
Vous utilisez le code suivant pour le faire.
#include <stdio.h>
#include <stdlib.h>
int main()
{
int x, number, fac;
fac = 1;
printf("Enter a number:\n");
scanf("%d",&number);
if(number<0)
{
printf("Factorial not defined for negative numbers.\n");
exit(0);
}
for(x = 1; x <= number; x++)
{
if (number >= 0)
fac = fac * x;
else
fac=1;
}
printf("%d! = %d\n", number, fac);
}
Je ne pense pas que je l'emploierais dans la plupart des cas, mais une pratique bien connue et de moins en moins utilisée consiste à disposer d'un tableau de recherche. Si nous ne travaillons qu'avec des types intégrés, la mémoire atteinte est minime.
Juste une autre approche, pour rendre le poster conscient d’une technique différente. De nombreuses solutions récursives peuvent également être mémorisées dans lesquelles une table de recherche est remplie lorsque l'algorithme est exécuté, ce qui réduit considérablement le coût des futurs appels (un peu comme le principe de la compilation .NET JIT).
Pour les grands nombres, vous pouvez probablement vous en tirer avec une solution approximative, que tgamma vous donne (n! = Gamma (n + 1)) à partir de math.h. Si vous voulez des nombres encore plus grands, ils ne rentreront pas dans un double. Vous devez donc utiliser lgamma (journal naturel de la fonction gamma).
Si vous travaillez quelque part sans un C99 math.h complet, vous pouvez facilement faire ce genre de chose vous-même:
double logfactorial(int n) {
double fac = 0.0;
for ( ; n>1 ; n--) fac += log(fac);
return fac;
}
Solution simple:
unsigned int factorial(unsigned int n)
{
return (n == 1 || n == 0) ? 1 : factorial(n - 1) * n;
}
Le plus simple et efficace est de résumer les logarhitms. Si vous utilisez Log10, vous obtenez de la puissance et un exposant.
Pseudocode
r=0
for i form 1 to n
r=r+log(i)/log(10)
print "result is:", 10^(r-floor(r)) ,"*10^" , floor(r)
Vous devrez peut-être ajouter le code pour que la partie entière n'augmente pas trop et diminue donc la précision, mais le résultat sera correct même pour les très grandes factorielles.
Nous devons commencer à partir de 1 jusqu'à la limite spécifiée, par exemple n. Commencer à partir de 1*2*3...*n.
En c, je l'écris en tant que fonction.
main()
{
int n;
scanf("%d",&n);
printf("%ld",fact(n));
}
long int fact(int n)
{
long int facto=1;
int i;
for(i=1;i<=n;i++)
{
facto=facto*i;
}
return facto;
}
Exemple en C (C a été marqué, donc je suppose que c'est ce que vous voulez) en utilisant la récursivité
unsigned long factorial(unsigned long f)
{
if (f) return(f * factorial(f - 1));
return 1;
}
printf("%lu", factorial(5));
Je le ferais avec une table de calcul pré-calculée, comme l'a dit John. Ce serait plus rapide à calculer qu'une solution itérative ou récursive. Cela dépend de la rapidité avec laquelle n! croît, car le plus grand n! vous pouvez calculer sans déborder un unsigned long long (valeur maximale de 18 446 744 073 709 551 615) n’est que 20!, de sorte que vous n’avez besoin que d’un tableau de 21 éléments. Voici à quoi cela ressemblerait en c:
long long factorial (int n) {
long long f[22] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600, 6227020800, 87178291200, 1307674368000, 20922789888000, 355687428096000, 6402373705728000, 121645100408832000, 2432902008176640000, 51090942171709440000};
return f[n];
}
**I used this code for Factorial:**
#include<stdio.h>
int main(){
int i=1,f=1,n;
printf("\n\nEnter a number: ");
scanf("%d",&n);
while(i<=n){
f=f*i;
i++;
}
printf("Factorial of is: %d",f);
getch();
}