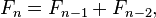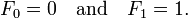Dans la séquence de Fibonacci, fib (0) ou 1?
Je fais une tâche dans un sujet où fib (0) est défini à = 1. Mais ça ne peut pas être vrai? fib (0) est 0?
Program with fib(0) = 1; spits out fib(4) = 5
Program with fib(0) = 0; spits out fib(3) = 3
Quelle est la définition correcte?
Vous avez raison. La séquence Fibonacci est définie avec les valeurs de départ fib(0) = 0 et fib(1) = 1. Ceci est une exigence pour que le reste de la séquence soit correct.
La seule condition dans laquelle fib(0) = 1 pourrait fonctionner est si vous avez défini un "système de comptage basé sur -1" (par opposition aux conventions habituelles de base à 0 et à base de 1). Ce serait assez loufoque cependant, je suis sûr que vous êtes d'accord.
La définition avec Fib (0) = 1 est appelée définition combinatoire et Fib (0) = 0 est la définition classique. Les deux sont utilisés dans Fibonacci Quarterly , bien que les auteurs qui utilisent la définition combinatoire doivent ajouter une phrase d’explication. Benjamin et Quinn dans les preuves qui comptent vraiment utilisent f_n pour le nième nombre de Fibonacci combinatoire et F_n pour le nième nombre de Fibonacci classique. La définition combinatoire est bonne, ce qui n’est pas surprenant si vous comptez des questions telles que "Combien de manières existe-t-il pour gravir n étapes en effectuant une ou deux étapes à la fois?" Lorsque n est égal à 0, il existe une façon de le faire, pas zéro.
À partir du numéro Fibonacci entrée sur Wikipedia:
En mathématiques, les nombres de Fibonacci sont la suite de nombres suivante:
Par définition, les deux premiers nombres de Fibonacci sont 0 et 1, et chaque nombre restant est la somme des deux précédents. Certaines sources omettent le 0 initial, mais commencent la séquence par deux 1 .
En termes mathématiques, la séquence Fn des nombres de Fibonacci est définie par la relation de récurrence
avec des valeurs de semences
Sur la base de la définition de la séquence de Fibonacci, vous pouvez générer un formulaire fermé pour définir le nième élément:
F(n) = ( f^n - (1-f)^n ) / sqrt(5),
where f = (1 + sqrt(5)) / 2 [the golden ratio]
Pour n = 0, il est clairement 0:
F(0) = (1 - 1) / sqrt(5) = 0.
http://en.wikipedia.org/wiki/Fibonacci_number
Fibonacci lui-même a commencé la séquence avec 1 et non pas 0. Il est important de reconnaître que l'opinion de chacun n'est pas un fait immuable, et il peut être intéressant de considérer que vous ne savez pas nécessairement mieux que celui qui a créé la séquence. Je pense que c'est bien de commencer la séquence avec 0 tant que vous n'agissez pas comme cela est la seule et unique façon de faire les choses, car le nombre à "index 0" est fondamentalement ambigu et doit toujours être communiqué explicitement .
La question de "l'indice" s'applique uniquement à nous et non à Fibonacci. Donc, si nous voulons utiliser son numéro de départ et que nous utilisons des index basés sur 0, nous placerions son numéro de départ à index 0 ou, si nous utilisons des index à 1, nous placerions son numéro de départ à index 1 .
Et comme il est en effet possible de continuer la séquence à gauche, cela rend aussi totalement arbitraire le début avec 0. Pourquoi ne pas commencer avec -1 et aller -1, 1, 0, 1, 1, 2 ...?
Ils sont tous les deux corrects. Si vous spécifiez une séquence G {n} par la récursivité G {1} = 3, G {2} = 5, G {n} = G {n - 1} + G {n - 2}, la plupart des gens s'accorderont pour dire que est "une séquence de Fibonacci". La seule différence est que quelques termes sont au début, mais les termes principaux ne sont généralement pas pertinents pour des questions intéressantes sur la séquence. Le cœur d'une séquence de Fibonacci est la règle d'addition, et toute séquence utilisant cette règle est une séquence de Fibonacci. Si vous souhaitez poser des questions spécifiques sur un index particulier, il suffit de spécifier si 0 est dans la séquence ... tout le reste n'est que la traduction de l'index et est en grande partie hors de propos. C'est-à-dire que si le problème est 'trouver une solution sous forme fermée pour la Nième valeur de la séquence', sa résolution pour G résoudra le problème pour F simplement en déplaçant la solution de manière triviale. La partie difficile du problème est la même pour les deux séquences.
Vous ne pouvez pas avoir zéro lapin et donc produire une paire, et "combien de paires de lapins peuvent être produites dans une année en commençant par une paire et en se reproduisant mensuellement à partir du deuxième mois" était la question initiale posée à Fibonacci.
fib 0 = 0
fib 1 = 1
C'est la définition de la valeur de départ.