Le NHS a-t-il tort sur les mots de passe?
Un médecin du NHS que je connais a récemment dû faire son questionnaire de formation obligatoire en ligne, qui pose un tas de questions sur la pratique clinique, la sûreté et la sécurité. Ce même questionnaire aura été envoyé à tous les médecins de cette fiducie NHS.
Le questionnaire comprenait la question suivante:
Lequel des éléments suivants ferait le mot de passe le plus sûr? Sélectionnez-en un:
une. 6 lettres, y compris minuscules et majuscules.
b. 10 lettres un mélange de majuscules et minuscules.
c. 7 caractères comprenant un mélange de chiffres, de lettres et de caractères spéciaux.
ré. 10 lettres tout en majuscules.
e. 5 lettres toutes en minuscules.
Ils ont répondu "b" et ils ont perdu une note, car la "bonne réponse" était apparemment "c".
Je crois comprendre qu'en règle générale, l'extension de la longueur du mot de passe ajoute plus d'entropie que l'extension de l'alphabet. Je suppose que le NHS pourrait faire valoir que les gens forment normalement de longs mots de passe à partir de mots très prévisibles, ce qui les rend faciles à deviner. Mais si vous forcez les gens à introduire des "caractères spéciaux", ils ont également tendance à les utiliser de manière très prévisible avec laquelle les algorithmes de devinette de mot de passe n'ont aucun problème.
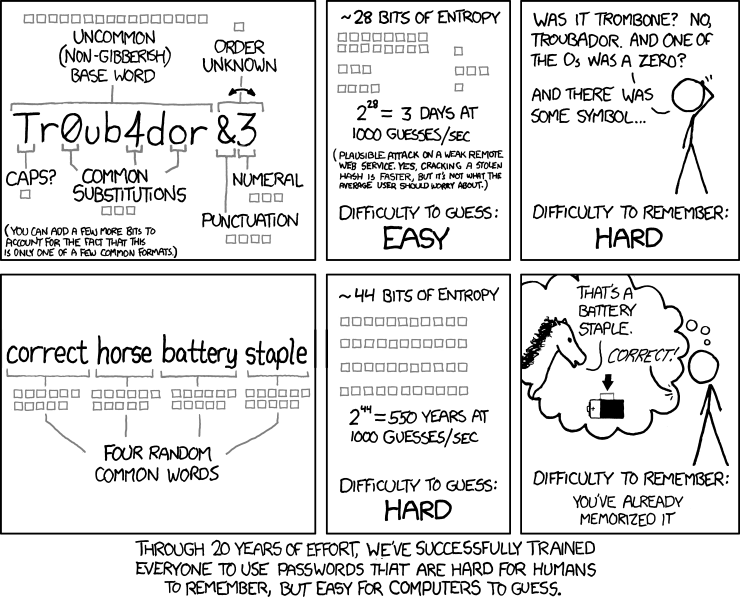
Bien que divulgation complète, je ne suis pas un expert des mots de passe - j'ai surtout eu cette impression de Randall Munroe (cliquez pour la discussion):
Ai-je tort?
De toute façon, ils ont tort:
Sept ASCII imprimables aléatoires: 957 = 69 833 729 609 375 mots de passe possibles.
Dix alphabétiques aléatoires: 52dix = 144 555 105 949 057 024 mots de passe possibles, soit plus de 2000 fois plus.
La longueur compte. Si vous générez vos mots de passe au hasard, cela compte beaucoup plus que toute autre méthode pour les rendre difficiles à deviner.
La perspective théorique
Faisons le calcul ici. Il y a 26 lettres, 10 chiffres et disons environ 10 caractères spéciaux. Pour commencer, nous supposons que le mot de passe est complètement aléatoire (et qu'un caractère dans un groupe n'est pas plus susceptible d'être utilisé qu'un caractère dans un autre groupe).
Le nombre de mots de passe possibles peut alors être écrit comme C = s^n où s est la taille de l'alphabet et n le nombre de caractères. L'entropie du mot de passe est définie comme:
log2(C) = log2(s^n) = log2(s)*n
Permet de brancher les chiffres de la question dans ceci:
s n Entropy (bits)
A 52 6 34.2
B 52 10 57.0
C 72 7 43.2
D 26 10 47.0
E 26 5 23.5
Donc, dans ce scénario, C n'est que la troisième meilleure option, après B et D.
La perspective pratique
Mais tout cela sous l'hypothèse de l'aléatoire. Ce n'est pas une hypothèse raisonnable sur la façon dont les gens génèrent des mots de passe. Les humains ne le font tout simplement pas de cette façon. Il nous faudrait donc choisir d'autres hypothèses sur la façon dont les mots de passe sont générés et l'ordre dans lequel l'attaquant les essaie dans son dictionnaire.
Une supposition non déraisonnable serait que de nombreux dictionnaires commencent par des mots et ne passent ensuite qu'à des substitutions et à l'ajout de caractères spéciaux. Dans ce cas, un seul caractère spécial dans un mot de passe court serait mieux qu'un mot commun très long. Mais d'un autre côté, si l'attaquant sait qu'un caractère spécial est toujours utilisé, il essaiera d'abord ces mots de passe. Et d'un autre côté, le dictionnaire est peut-être centré sur des principes complètement différents (comme l'occurrence dans les bases de données divulguées).
Je pourrais continuer à spéculer pour toujours.
Pourquoi c'est la question, pas les réponses, qui est fausse
Le problème est qu'il existe de nombreux principes de sélection du mot de passe, et je pourrais en choisir un arbitrairement pour que presque toutes les réponses soient correctes. Donc, toute la question est inutile et ne sert qu'à masquer un point important qu'aucune politique de mot de passe dans le monde ne peut appliquer: Ce n'est pas quels caractères un mot de passe contient qui le rend fort - c'est comment il est généré.
Par exemple, Password1! contient des majuscules, des minuscules, un nombre et un caractère spécial. Mais ce n'est pas très aléatoire. ewdvjjbok d'autre part ne contient que des minuscules mais est beaucoup mieux car il est généré aléatoirement .
Ce qu'ils auraient dû faire
Si vous arrêtez simplement de vous fier à la mémoire humaine très faillible et limitée, le jeu de caractères et la longueur cessent d'être des facteurs limitants que vous devez peser les uns contre les autres. Vous pouvez avoir les deux en abondance.
Pour ce faire, vous pouvez utiliser un gestionnaire de mots de passe. Comme Dan Lowe l'a souligné dans les commentaires, cela pourrait ne pas être une option réalisable dans un hôpital. Une deuxième alternative consiste à utiliser une sorte d'authentification à deux facteurs (par exemple un jeton matériel ou une carte-clé) qui rend la sécurité du premier facteur (le mot de passe) moins importante.
C'est la responsabilité des gestionnaires de système, et non des utilisateurs finaux, à mettre en œuvre. Ils doivent fournir les outils qui permettent aux utilisateurs finaux d'effectuer leur travail de manière pratique et sûre. Aucune formation des utilisateurs ne peut changer cela.
Je me rends compte qu'il existe déjà un certain nombre de bonnes réponses, mais je veux clarifier un point.
La question est sans réponse car elle ne spécifie pas de jeu de caractères, ni de méthode de sélection de mot de passe.
Tout d'abord pour aborder le deuxième point, nous prétendrons que les mots de passe sont générés de manière vraiment aléatoire dans le domaine autorisé, sinon nous ne pourrons même pas commencer à raisonner sur la question.
Pour notre autre point, pour donner des exemples extrêmes, disons que b implique des lettres uniquement dans l'alphabet anglais, donc disons 52 symboles possibles. Cela donne environ 5,7 bits d'entropie par caractère et donc environ 57 bits d'entropie au total.
D'autre part, disons (peut-être un peu déraisonnablement) que la réponse c implique tout point de code Unicode complètement aléatoire qui est considéré comme un caractère (par opposition à une nomenclature, etc.). Il y en a actuellement environ 109 000 en Unicode 6. Cela signifie environ 16,7 bits d'entropie par caractère et un total de 117 bits d'entropie.
D'un autre côté, si la réponse c était limitée à seulement ASCII ou peut-être ISO 8859-15 ou un sous-ensemble de ceux-ci, la conclusion opposée pourrait facilement être tirée.
Ceci est bien sûr complètement déraisonnable, mais met en évidence la fragilité de la question et comment on peut raisonnablement justifier l'une ou l'autre réponse. Pour être une question de test sensée, elle devrait être formulée beaucoup plus rigoureusement, ce qui rendrait beaucoup plus difficile le travail des utilisateurs ayant des connaissances techniques ou mathématiques limitées.
En fin de compte, je dirais que ce test est probablement assez inutile car une organisation n'exigerait idéalement pas que les utilisateurs mémorisent les exigences de mot de passe, mais les appliqueraient plutôt sur le plan technologique (la seule exigence à laquelle je pense que l'apprentissage par cœur est utile n'est pas de réutiliser le même mot de passe à plusieurs endroits).
Le NHS se trompe-t-il sur les mots de passe les plus sécurisés dans le cas idéal? Oui, absolument - et les autres réponses ont assez bien couvert ce sujet.
Le NHS se trompe-t-il sur les mots de passe les plus sécurisés dans un environnement NHS? Peut être pas.
Comment un mot de passe long pourrait-il être pire que ...?
Il existe des systèmes hérités qui limitent artificiellement la longueur d'un mot de passe - par exemple, l'ancien hachage de mot de passe Windows LANMAN/NTLMv1 limite la longueur à 14 symboles, et l'ancien hachage de mot de passe UNIX basé sur DES la limite à 8. Pire, le mot de passe l'entrée sur un tel système vous permettra souvent de saisir un mot de passe aussi longtemps que vous le souhaitez, et d'ignorer tout après les premiers n symboles.
En fait, il semble probable que NTLMv1 soit le schéma hérité particulier qu'ils exécutent. Comme le souligne @MarchHo, NTLMv1 divise votre mot de passe en deux moitiés de 7 caractères chacune au maximum, et chaque moitié peut être craquée séparément. Donc, si vous utilisez NTLM avec un mot de passe alphanumérique à 10 caractères, ce que vous avez vraiment, c'est un mot de passe alphanumérique à 7 caractères et un mot de passe alphanumérique à 3 caractères. Le premier est clairement pire que 7 caractères du jeu de symboles complet, et le dernier peut être cassé en millisecondes sur un PC de 10 ans.
Pourquoi quelque chose d'aussi ancien serait-il encore couramment utilisé?
Fondamentalement, car cela fonctionne et sa mise à niveau coûterait cher.
Maintenant, c'est moi qui spécule, mais: je propose que les environnements de soins de santé en particulier soient susceptibles d'exécuter des systèmes hérités, en raison de la nature sensible des soins de santé. Les nouveaux systèmes nécessiteront probablement un examen très approfondi avant d'être acceptés comme solution, ce qui signifie que les mises à niveau des systèmes de santé ont tendance à se produire lentement et à grands frais.
Donc, si vous savez qu'il existe des systèmes couramment utilisés qui se comportent de cette façon et que vous ne pouvez pas les corriger, le mieux que vous puissiez faire est de dire à vos utilisateurs de choisir une longueur - n mot de passe utilisant le plus grand pool de symboles possible.
En général: êtes-vous sûr que vos mots de passe ne sont pas tronqués?
Malheureusement, cela a également des implications pour le cas général, en particulier pour nous qui aimons nos mots de passe depuis longtemps. Dans quelle mesure sommes-nous sûrs que nous ne pouvons pas nous connecter à notre compte sur https://example.com avec juste le premier mot ou deux de notre phrase secrète? Aussi mauvais que d'utiliser le "correcthorsebatterystaple" bien connu, utiliser accidentellement "correct" serait encore pire. Pour être sécurisé dans vos mots de passe, il ne suffit pas de vous assurer de générer suffisamment d'entropie. Vous devez également être sûr que le système à l'autre bout ne jette pas la majeure partie de celui-ci.
Il y a quelques problèmes avec cette question. L'un d'eux est qu'il ne précise pas comment les mots de passe sont choisis, mais je pense que l'approche la plus logique est de supposer que les mots de passe sont choisis au hasard mais satisfaisant aux conditions respectives, donc j'utiliserai cette convention pour ma réponse. Notez que la bande dessinée de Randall ne partage clairement pas cette hypothèse, mais la question ne spécifiait pas la façon dont un mot de passe est choisi, donc je pense que nous pouvons opter pour le meilleur qui soit possible et c'est choisir un mot de passe au hasard. De plus, le test n'est probablement pas basé sur la bande dessinée de Randall.
Le rythme clé de l'option b est assez facile à calculer si nous supposons que l'alphabet anglais est utilisé. Ouais, plus d'hypothèses, je sais. Mais puisque le test semble être en anglais et pas très difficile, je pense que nous pouvons faire cette hypothèse.
Il y a 26 lettres minuscules dans l'alphabet anglais et autant de lettres majuscules, soit 52 au total. Il y a donc 52 ^ 10 ≈ 1,45 * 10 ^ 17 éléments dans l'espace clé de l'option b.
L'option c est beaucoup moins spécifique que l'option b. Cependant, puisque nous avons supposé que l'alphabet anglais est utilisé - ce qui est en faveur de l'option c - nous pouvons également supposer que seul ascii est utilisé pour les caractères spéciaux - ce qui est en faveur de l'option b. Vraiment, si nous supposions plus de caractères spéciaux que ascii, nous devrons supposer plus de lettres que dans ascii puisque ä est sans doute une lettre en allemand. Cela rend l'espace clé de l'option b encore plus grand par rapport à celui de l'option c. *
Le mieux que nous puissions faire pour l'option c si nous nous limitons à l'alphabet ascii est d'utiliser tous les caractères imprimables (à l'exception du blanc) dans notre alphabet (note: utilisation différente et plus générale du mot "alphabet") . Cela fait 94 caractères, donnant à l'option c un espace clé de 94 ^ 7 ≈ 6,48 * 10 ^ 13 éléments.
Étant donné que l'une de nos hypothèses pour résoudre la question est que le mot de passe est choisi au hasard avec les restrictions respectives et que la règle est égale au choix d'un mot de passe au hasard dans l'espace clé respectif, un mot de passe choisi en utilisant l'option b est sans doute plus difficile à deviner car il existe plusieurs ordres de grandeur plus d'options à essayer lors du crackage du mot de passe.
En fait, si nous supposons que les coûts de la fissuration d'un mot de passe via la force brute sont approximativement linéaires par rapport à la taille de l'espace clé, la fissuration d'un mot de passe choisi via l'option b est de 52 ^ 10/(94 ^ 7) ≈ 2'229 fois plus dur que le cracking choisi via l'option c, montrant clairement que la réponse prétendument correcte à cette question est fausse.
* C'est assez facile à prouver mathématiquement mais ce StackExchange manque de support LaTeX et vous le comprendrez probablement mieux grâce à une description textuelle de toute façon.
La seule option d'avantage c par rapport à l'option b est son plus grand alphabet (encore une fois, une utilisation plus générale du mot "alphabet"). L'option b, cependant, fait plus que compenser en choisissant un mot de passe plus long. Si nous ajoutons de plus en plus de caractères (comme ü, à, Ø, Æ, etc.), nous améliorons la taille des alphabets, ce qui réduit l'avantage de c sur b, tandis que l'avantage de b over c n'est pas affecté.
J'adore les questions d'entropie:
La réponse courte:
Oui, vous avez "techniquement" raison d'avoir plus d'entropie (le meilleur type de correct).
La réponse longue
L'entropie est largement prise en compte par deux choses. Nombre de symboles qu'un mot de passe peut utiliser et longueur. Dans le scénario du NHS, il serait logique que les "caractères spéciaux" soient des symboles disponibles à utiliser dans la réponse à 10 caractères et, par conséquent, plus un mot de passe est long, plus l'entropie est élevée et théoriquement plus sûr.
TOUTEFOIS, nous devons traiter avec des gens et nous sommes paresseux. La question est d'essayer d'amener les gens à inclure des caractères spéciaux dans leur mot de passe car cela force l'entropie à se produire.
Sans cela, la bande dessinée de Randall est mathématiquement correcte, tout en étant effrontée, mais tout SysAdmin qui pense que correcthorsebatterystapler est un bon mot de passe car il doit longtemps être giflé, car cela fait partie de mes tables Rainbow depuis un certain temps.
Pour être juste, je pense que prendre quatre mots du dictionnaire et les enchaîner est un bon concept (c'est ce que nous appelons une phrase secrète), mais les gens comme je l'ai dit sont paresseux et tomberont probablement pour des modèles communs.
Le test cité et vos contre-arguments sont tous deux erronés, essentiellement parce que l'entropie est une mesure de caractère aléatoire d'un mot de passe - pas de la longueur, pas de la taille de l'alphabet. Le schéma de bandes dessinées XCKD que vous citez est sécurisé au niveau de sécurité de 44 bits revendiqué si et seulement si les 44 petites cases grises sous "agrafe de batterie de cheval correcte" représentent les résultats des tours de pièces (ou uniforme similaire, événements aléatoires indépendants) qui ont été utilisés pour sélectionner les mots de passe. Si un humain choisit les mots, tous les paris sont annulés.
Étant donné que ni le NHS ni vous ne parlez de ce facteur critique, il est impossible de dire quoi que ce soit de concret sur la sécurité des mots de passe, sinon s'ils ne sont pas choisis uniformément au hasard, ils sont probablement faibles.
Je crois comprendre qu'en règle générale, l'extension de la longueur du mot de passe ajoute plus d'entropie que l'extension de l'alphabet.
Si d est la taille de l'alphabet et n est la longueur du mot de passe, alors un mot de passe choisi uniformément au hasard a log2(d) * n bits d'entropie. Le doublement de la taille de l'alphabet ajoute donc n bits d'entropie; l'ajout d'un symbole supplémentaire au mot de passe ajoute log2(d) bits. Tout se résume donc aux valeurs concrètes de d et n; il est vraiment très inutile d'avoir une règle de base comme vous le proposez, car nous pouvons simplement calculer les augmentations de manière simple.
Voici la chose, que cela vous plaise ou non, cette question ne concerne pas le laboratoire ou les mots de passe mathématiquement plus sécurisés. Il s'agit d'amener les gens à "penser" à leurs mots de passe lorsqu'ils les choisissent.
une. Est incorrect car il ne contient que des lettres.
b. est faux car il n'a que des lettres
c. est correct car il est suffisamment long et comprend des "caractères spéciaux"
ré. est faux car il n'a que des lettres.
Ou en d'autres termes, les mots de passe utilisant uniquement des lettres sont mauvais.
Maintenant, il est vrai que vous pouvez créer un mot de passe plus sécurisé en utilisant uniquement des lettres s'il est assez long ou aléatoire. Certes, "asefhesesnh" est meilleur que "p4ssw0rd!", Mais pour être honnête, c'est une compréhension au-delà de la plupart des gens dans le public cible de ce test.
Au lieu de cela, il est "préférable" de faire comprendre aux utilisateurs de choisir un mot de passe qui est "plus long" et qui a des lettres, des chiffres et des caractères spéciaux.
En d'autres termes, C est correct lorsque vous parlez d'un large éventail d'utilisateurs avec différents niveaux de compétences techniques, créant leurs propres mots de passe. Bien sûr, les calculs peuvent être erronés, mais cela n'a pas d'importance. Aucun fournisseur ne va rester là et comprendre l'entropie des mots de passe, mais ils peuvent compter le nombre de $ dans un mot de passe.
L'option b vous offre 52 possibilités par personnage.
Pour que c soit meilleur, chacun des 7 caractères doit avoir plus de 5210/7 = au moins 283 possibilités.
Cela signifie ASCII ou les jeux de caractères ANSI occidentaux ne suffiront pas. Ils devraient autoriser le jeu de caractères Unicode (ou certaines pages de codes ANSI asiatiques très obscures) pour que l'option c soit meilleure.
C'est évidemment une question mal formulée. Il y a 62 chiffres et lettres (majuscules + minuscules) donc la bonne réponse serait:
c si 'caractères spéciaux' signifie que je peux utiliser des caractères Unicode ou tout autre jeu de caractères contenant au moins 221 caractères non alphanumériques (c'est-à-dire 'spéciaux'), sinon b.