Lors du choix d'un code PIN numérique, est-il utile ou nuisible de rendre chaque chiffre unique?
Imaginez un schéma à quatre chiffres PIN contenant les chiffres [0-9]. Si je choisis mon PIN au hasard, j'en obtiendrai un sur 10 * 10 * 10 * 10 = 10 000 codes. D'après ma propre expérience, plus de la moitié du temps, une séquence aléatoire de quatre chiffres contiendront une propriété ou un motif qui réduit considérablement son entropie: un seul chiffre utilisé dans plus d'une position, un motif ascendant/descendant, etc. (Oui, oui, un 4 chiffres PIN uniquement a quelque chose comme 13 bits d'entropie max pour commencer, mais certains codes aléatoires sont encore plus horribles .)
Si je respectais une règle où j'utilise uniquement un PIN qui a un chiffre unique dans chaque position, je crois que le nombre de codes à ma disposition devient 10 * 9 * 8 * 7 = 5,040 (quelqu'un s'il vous plaît corrigez-moi si je me trompe.) J'ai presque réduit de moitié mon espace clé, mais j'ai également éliminé de nombreux codes à entropie inférieure de la considération.
À la fin de la journée, est-ce que je me suis aidé ou me suis blessé en faisant cela?
EDIT: Wow, beaucoup de bonnes réponses ici. À titre de clarification, je pensais à l'origine moins en termes de guichet automatique/banque PIN (qui a probablement une politique de verrouillage agressive après un certain nombre de suppositions incorrectes) et plus en termes d'autres " dispositifs à code PIN non supervisés: serrures de porte programmables, panneaux de système d'alarme, claviers de porte de garage, etc.
Le truc, c'est qu'avec une broche à 4 chiffres, l'entropie n'est pas vraiment importante. Ce qui est important c'est le lock-out et la psychologie de l'attaquant.
L'espace de clé est si petit que toute attaque automatisée (sans verrouillage) l'épuiserait presque instantanément.
Ce qui vous inquiète, c'est qu'un attaquant devine le code PIN avant le verrouillage du compte. Donc, en supposant un verrouillage sain (disons 3-5 tentatives incorrectes), vous voulez que votre PIN soit en dehors des 3-5 les plus susceptibles d'être choisis PIN).
Personnellement, j'éviterais toute séquence répétitive à 4 chiffres et tout ce qui commence en 19XX, ce qui serait un an de naissance.
Maintenant, les alecs intelligents diront "ahh mais si vous faites cela, les attaquants sauront ne pas essayer ceux-ci", mais cela ne s'applique que si a) la majorité de la population d'utilisateurs suit ce conseil (indice, ils ne le feront probablement pas) et b) les attaquants savent que la population d'utilisateurs a suivi ce conseil.
Une grande analyse de cela (lien gracieuseté de @codesincahaos)
Edit 2 - Pour une interprétation beaucoup plus mathématique de ce que je recommanderais de lire @ réponse de diagprov
Je vais faire irruption et parler un peu d'entropie et de probabilité et j'espère que cela vous aidera à comprendre.
Premièrement, quelle est la probabilité? C'est en fait une question ouverte parmi les statisticiens mais voici la définition fréquentialiste: nous disons que si une pièce de monnaie équitable est retournée, elle a une probabilité de 0,5 de monter des têtes. Cependant, si vous lancez une pièce, vous remarquerez peut-être que les cinq premiers résultats sont tous des têtes, ce qui ne semble pas correct. Donc, le fréquencialiste dit que si vous renversiez la pièce "assez" fois , vous découvrirez finalement qu'un sur deux des lancers de pièces sont des têtes.
La clé est que la probabilité ne dit rien sur ce qui se passera réellement . Un mot de passe à haute entropie pourrait être deviné dès le premier essai par simple chance, quels que soient les résultats possibles, etc.
Maintenant, qu'est-ce que l'entropie? Si vous avez commencé à dire "c'est le nombre de résultats possibles ...", vous avez peut-être raison dans un contexte de génération de données aléatoires, mais c'est l'exemple parfait où vous avez vraiment besoin de comprendre ce qui se passe en dessous.
Parlons d'abord de l'auto-information. Il s'agit d'une variable aléatoire (ce qui signifie qu'il existe un certain nombre de résultats possibles) qui varie sur la probabilité de chaque résultat (puis nous prenons -log2 (P (X)) pour le coder en "bits" d'informations). Nous devons donc attribuer à chaque résultat une probabilité.
Comme d'autres l'ont souligné, certaines variations de PIN choix sont plus probables. Tous les mêmes numéros (1111, 2222, 3333, ...), anniversaires (20XX, 19XX) et ainsi de suite. Vous devriez attribuer une probabilité plus élevée à ces chiffres, car les gens sont tout simplement plus susceptibles de les choisir et ne choisiront certainement pas une séquence aléatoire. La façon dont vous attribuez la probabilité à d'autres nombres dépend entièrement de vous et dépend vraiment de ce que vous savez le processus de choix d'une épingle.
Maintenant, l'entropie, ou pour garder @codesinchaos heureux, l'entropie de Shannon en particulier, est la moyenne de la auto information distribution . C'est la valeur "la plus probable" de l'auto-information étant donné les probabilités de chaque choix . Qu'est-ce que ça veut dire? Comme le dit la réponse actuellement la mieux notée, c'est une mesure du processus de choix et de sa qualité, pas de l'épingle elle-même.
Que se passe-t-il lorsque vous souscrivez des choix à forte probabilité comme 1111, 2222, 3333? Ces résultats donnent une auto-information très faible (-log (P (X)) est petit pour les grandes probabilités, car nous nous attendons à ce qu'ils se produisent) et donc les supprimer déplace la distribution vers la droite, c'est-à-dire déplace l'emplacement de la distribution vers centre. Cela augmentera sa moyenne. Ainsi, supprimer les choix que la plupart des gens feraient autrement avec une probabilité élevée augmente en fait l'entropie .
Regardons l'entropie d'une manière différente: si vous deviez deviner les codes PIN, dans quel ordre les essayeriez-vous (en supposant qu'il n'y ait pas de verrouillage)? Vous commenceriez certainement avec les codes PIN les plus probables. Ce que l'entropie dit, c'est que si vous répétez cette expérience suffisamment de fois (c'est-à-dire que vous essayez de deviner le PIN d'un grand nombre de cartes dont les PIN ont été choisis avec la même logique exacte)), alors un choix d'entropie plus faible vous donnerait, l'attaquant, le succès plus rapidement.
Encore une fois, cela reste une question de ce qui se passe pourrait dans le cas théorique de nombreuses cartes, pas ce qui se passe pourrait parce que l'attaquant a de la chance.
Voici votre résumé:
- L'entropie dépend de la façon dont vous affectez les probabilités à l'espace de résultat.
- Sans aucun doute, si vous laissez les humains choisir des codes PIN, ils choisiront certaines valeurs avec une probabilité beaucoup plus élevée que d'autres.
- Cela signifie que vous ne pouvez pas supposer que la distribution sous-jacente est uniforme et dire "entropie == nombre de résultats".
- Si vous supprimez les options de mauvais choix les plus probables, l'entropie augmente.
- L'entropie, comme la probabilité de deviner correctement, ne dit absolument rien si un attaquant aura de la chance et devinera correctement votre PIN. Il dit simplement qu'en théorie, une meilleure entropie donne à votre attaquant un temps plus difficile.
Maintenant, pour compléter ma réponse, examinons les aspects pratiques. Si nous allons comparer des mots de passe, ou des choix de sortie de fonction de hachage, ou des données aléatoires, les codes PIN sont nuls. Si vous donnez à un attaquant et à un défenseur le libre choix de PIN devinez et aucune autre information, le nombre de suppositions pour avoir raison 50% du temps (paradoxe d'anniversaire) est ridiculement bas. Les PINs feraient moche fonctions de hachage.
Cependant, les humains ne peuvent pas très bien mémoriser 128 bits de données, surtout lorsqu'ils sont ivres et essaient de payer pour un kebab en utilisant la puce et la broche. Les codes PIN sont donc un compromis pragmatique et avec trois suppositions comme limite, à part un attaquant qui a beaucoup de chance, vous devriez être en sécurité.
TL; DR Supprimer le choix des codes PIN les plus probables de vos choix possibles améliore vos chances face à un attaquant qui ne devinera pas au hasard (c'est-à-dire la plupart des attaquants).
Edit: Je pense que cette discussion justifie maintenant quelques mathématiques. Voici ce que je vais supposer dans mes calculs:
- Nous utilisons des codes PIN à 4 chiffres
Les données du lien de Raesene sont correctes, c'est-à-dire que:
#1 1234 10.713% #2 1111 6.016% #3 0000 1.881% #4 1212 1.197% #5 7777 0.745% #6 1004 0.616% #7 2000 0.613% #8 4444 0.526% #9 2222 0.516% #10 6969 0.512% #11 9999 0.451% #12 3333 0.419% #13 5555 0.395% #14 6666 0.391% #15 1122 0.366% #16 1313 0.304% #17 8888 0.303% #18 4321 0.293% #19 2001 0.290% #20 1010 0.285%- Je vais également supposer que tout PIN non mentionné dans cette liste a une chance égale d'être choisi parmi la probabilité restante "non allouée" (1 probabilité totale consommée ci-dessus). C'est presque certainement incorrect, mais nous ne disposons que de tant de données.
Pour calculer cela, j'ai utilisé le code sage suivant:
def shannon_entropy(probabilities):
contributions = [p * (-1*log(p,2)) for p in probabilities]
return sum(contributions)
Calcule l'entropie réelle de Shannon pour un ensemble donné de probabilités.
import itertools
total_outcomes = 10.0^4
probability_random_outcome = 1 / total_outcomes
probability_random_outcome
maximum_entropy = -log(probability_random_outcome, 2)
maximum_entropy
maximum_entropy_probability_list = list(itertools.repeat(probability_random_outcome, total_outcomes))
maximum_entropy_calculated = shannon_entropy(maximum_entropy_probability_list)
print(maximum_entropy)
print(maximum_entropy_calculated)
Démontre que ma fonction calcule avec précision l'entropie maximale, en prenant une liste de 10 ^ 4 probabilités, chacune à 1/10 ^ 4.
Alors
probability_list_one = [10.713/100, 6.016/100, 1.881/100, 1.197/100, 0.745/100, 0.616/100, 0.613/100, 0.526/100,0.516/100, 0.512/100, 0.451/100, 0.419/100, 0.395/100, 0.391/100, 0.366/100, 0.304/100, 0.303/100,0.293/100,0.290/100,0.285/100]
outcome_count_one = 10^4 - len(probability_list_one)
print("Outcome count 1:", outcome_count_one)
probability_consumed_one = sum(probability_list_one)
print("Probability consumed by list: ", probability_consumed_one)
probability_ro_one = (1-probability_consumed_one)/outcome_count_one
entropy_probability_list_one = probability_list_one + list(itertools.repeat(probability_ro_one, outcome_count_one))
entropy_one = shannon_entropy(entropy_probability_list_one)
entropy_one
Ici, comme je l'ai dit ci-dessus, je prends ces 20 probabilités et je suppose que les autres probabilités sont réparties uniformément entre les résultats restants, en étendant la liste avec chaque probabilité définie de manière égale. Le calcul est effectué.
probability_list_two = [6.016/100, 1.881/100, 1.197/100, 0.745/100, 0.616/100, 0.613/100, 0.526/100,0.516/100, 0.512/100, 0.451/100, 0.419/100, 0.395/100, 0.391/100, 0.366/100, 0.304/100, 0.303/100,0.293/100,0.290/100,0.285/100]
outcome_count_two = 10^4 - len(probability_list_two)-1
print("Outcome count 2:", outcome_count_two)
probability_consumed_two = sum(probability_list_two)
print("Probability consumed by list: ", probability_consumed_two)
probability_ro_two = (1-probability_consumed_two)/outcome_count_two
entropy_probability_list_two = probability_list_two + (list(itertools.repeat(probability_ro_two, outcome_count_two)))
entropy_two = shannon_entropy(entropy_probability_list_two)
entropy_two
Dans ce cas, je supprime le code PIN le plus probable, 1111 et recalcule l'entropie.
À partir de ces résultats, vous pouvez voir que le choix aléatoire d'un PIN a 13,2877 bits d'entropie. La répétition de cette expérience avec un PIN supprimé nous donne 13,2876 bits
Choisir un PIN compte tenu de ces probabilités de choix pour ces 20 PIN et autrement choisir au hasard signifie que votre choix est de 11,40 bits d'entropie, sur un possible de 13,2877 bits. À partir de cette base, bloquer PIN 1111 et permettant autrement les 19 PIN restants évidents et tous les autres PIN choisis avec une probabilité égale a une entropie de 12,33 bits, sur un possible de 13,2876 bits.
J'espère que cela explique pourquoi de nombreuses réponses disent que l'entropie est en baisse plutôt qu'en hausse. Ils envisagent l'entropie maximale possible, plutôt que l'entropie moyenne (entropie shannon) du système en tenant compte de la possibilité de choix. Une meilleure mesure est l'entropie shannon, car elle prend en compte la probabilité que chaque choix soit fait globalement et donc la façon dont un attaquant procédera probablement à l'attaque.
Comme vous pouvez le voir, le blocage de ce PIN 1111 augmente considérablement l'entropie shannon, à un léger coût pour l'entropie globale possible. Si vous voulez discuter de l'entropie, en gros, supprimer le PIN 1111 aide massivement.
Pour référence cette bande dessinée XKCD calcule l'entropie des mots de passe pauvres à environ 28 bits et l'entropie des bons plus haut, à 44 bits. Encore une fois, cela dépend des hypothèses qui sont faites quant aux probabilités de certains choix mais cela devrait également montrer que les NIP sont nuls en termes d'entropie et que la limite de N-essais pour le petit N est la seule raison façon de procéder.
Cela dépend vraiment de la façon dont le PIN est créé:
Si le PIN est généré , assurez-vous que la distribution est uniforme et n'excluez aucune combinaison. Cela maximisera l'entropie.
Si le PIN est choisi par un opérateur humain, il est parfaitement logique d'exclure certaines combinaisons. Je ne le ferais pas allez jusqu'à rejeter la moitié des combinaisons, mais si vous le faites, vous devriez également envisager de rejeter les codes PIN commençant par
01et2(pensez aux années et dates de naissance), puis les codes PIN correspondant aux dispositions de clés physiques comme2580et1379et ainsi de suite. Assurez-vous simplement de vous arrêter avant de finir par autoriser une seule8068PIN qui cette étude s'est avéré le moins probable.
Ce que vous devriez faire pour les codes PIN choisis par l'homme exclut les combinaisons les plus courantes: 1234 et 1111 représente à lui seul près de 17% de tous les codes PIN utilisés et les 20 codes PIN les plus populaires représentent près de 27%. Ceux-ci incluent chaque chiffre répété 4 fois et des combinaisons populaires comme 1212 et 4321.
Edit: sur une seconde réflexion, je pense que vous devriez exclure les combinaisons les plus courantes dans tous les cas. Même si votre PIN est généré de manière aléatoire, l'attaquant peut ne pas le savoir, auquel cas il tentera très probablement ces combinaisons en premier.
L'entropie est une propriété de la méthode de génération de mot de passe, pas le mot de passe.
Si vous décidez d'éliminer les chiffres répétés - cette décision réduit l'entropie par rapport à la génération d'une séquence aléatoire.
En fait, tout ce que vous proposez aura une entropie plus faible que la génération d'une séquence aléatoire.
Et si vous croyez qu'un mot de passe généré aléatoirement 1111 a une faible entropie et est donc plus facile à utiliser par force brute, il suffit d'aller dans n'importe quel lieu de jeu et de parier sur 1 quatre fois de suite - ce devrait être une victoire sûre.
Limiter votre pool de numéros disponibles réduit le nombre de solutions possibles, ce qui le rend moins sûr.
La répétition des chiffres est une faiblesse humaine courante lors du choix des codes PIN, ce qui signifie qu'elle sera d'abord essayée par les attaquants. Ainsi, écarter les chiffres répétés augmente la sécurité.
Comme c'est souvent le cas, la décision a des avantages et des inconvénients selon l'attaque spécifique contre laquelle vous vous défendez. Vous ne devriez probablement pas trop y penser et envisager des changements de perspective plus large (comme ne pas utiliser une broche à 4 chiffres, ou ajouter un deuxième facteur, ou avoir des verrouillages lors d'essais incorrects) si vous souhaitez augmenter la sécurité du système.
Il me semble que la plupart des autres réponses se concentrent sur le mauvais type d'attaque.
Comme nous avons affaire à un scénario très spécifique (manuel PIN), nous pouvons optimiser la génération PIN) pour les scénarios d'attaque possibles.
attaque de dictionnaire
D'après ce que je peux tirer de la question, nous parlons de saisie manuelle PIN, donc l'attaquant doit taper chaque PIN ils essaient. Donc, une brute l'attaque forcée peut prendre un certain temps (disons, vous avez besoin de deux secondes pour chaque PIN vous essayez, cela prendra presque trois heures en moyenne). C'est possible, mais pas l'approche la plus intelligente.
Ainsi, lorsqu'une attaque par force brute est impossible, vous pouvez plutôt essayer une attaque par dictionnaire. Ici, vous essayez d'abord les codes PIN les plus courants. Si cela échoue, vous pouvez toujours recourir à une attaque par force brute plus tard. Avec les attaques par dictionnaire, l'entropie n'a plus vraiment d'importance. Ici, il importe que le mot de passe soit dans le dictionnaire ou non. Étant donné que l'attaquant n'a probablement pas de véritable dictionnaire de codes PIN communs, il devra trouver son dictionnaire à la volée. Cela voudrait dire que le dictionnaire sera probablement plutôt court et orienté sur les modèles. Les codes PIN possibles dans le dictionnaire seraient:
- NIP consécutifs (par exemple 0123 ou 1234)
- PIN avec quatre fois le même chiffre (par exemple 2222)
- peut-être aussi des codes PIN avec seulement trois fois le même chiffre
En éliminant ces quelques mots de passe, vous ne réduisez pas beaucoup la taille de votre espace de clés, mais vous pouvez facilement vous défendre contre les attaques par dictionnaire. Des stratégies similaires sont utilisées par les sites Web qui ne vous permettent pas d'utiliser des mots de passe courants ou faciles à deviner (par exemple, en utilisant le nom d'utilisateur comme mot de passe)
Attaque de force brute
Ensuite, nous pouvons essayer d'optimiser contre d'éventuelles attaques par force brute. Cela pourrait aider beaucoup moins pour un coût plus élevé, donc cela pourrait ne pas valoir la peine. Il existe deux stratégies principales permettant à un attaquant humain d'effectuer des attaques par force brute: il suffit de saisir des codes PIN aléatoires ou de commencer par 0000 et de décompter (ou 9999 et décompter). Les codes PIN comme 0001 ou 9998 peuvent donc être un mauvais choix, car une personne effectuant une attaque par force brute peut les trouver assez rapidement. Alors peut-être exclure les codes PIN commençant par 0 ou 9.
En suivant ces règles, vous ne devriez pas perdre trop de mots de passe possibles, mais vous pourrez peut-être renforcer votre PIN contre les stratégies d'attaque les plus courantes pour ce scénario spécifique.
Je n'ai pas assez de commentaires mais j'ai une recommandation. PIN qui sont tapés à l'aide d'un seul bouton (ou d'un simple motif de boutons) sont plus facilement observés par un surfeur d'épaule. À l'école primaire, l'enseignant pensait qu'ils m'ont rendu service en créant mon mot de passe 4321 et une secousse a regardé mon doigt bouger en ligne droite et a dit à tout le monde mon mot de passe.
Je vous conseille de faire une liste des codes confidentiels faibles qui peuvent être séparés, puis de les soustraire des codes confidentiels générés de manière aléatoire.
Cela dépend de la mise en œuvre. L'élimination des nombres consécutifs réduira l'espace de clés de 0,1%, mais présente certains avantages pour la sécurité physique qui peuvent en valoir la peine.
Beaucoup de bien des réponses intelligentes ici, le point principal étant qu'au lieu de le rendre plus sécurisé, vous réduisez l'espace de clé (cependant de manière négative, 10 sur 10 000).
Les meilleures réponses ne parviennent cependant pas à aborder l'aspect physique de la saisie d'une épingle. L'extraction visuelle et thermovisuelle est un réel danger de nos jours. En d'autres termes, les méchants surfent sur votre code PIN avec leurs yeux, un télescope, une caméra écrémée sur le guichet automatique ou même des caméras thermiques.
Ce dernier est plus récent, et particulièrement désagréable car un skimmer peut marcher jusqu'à un tampon à épingles et regarder la signature thermique, même si vous avez bien couvert le tampon.
Avoir une épingle consécutive nuira à la sécurité dans ce domaine; il réduit la complexité de l'emplacement physique des nombres d'une quantité horrible. Même si vous avez couvert votre main, il est probable que l'attaquant devine le bouton sur lequel vous avez appuyé quatre fois avant le verrouillage. Sur un téléphone, s'il y a une grosse tache de graisse sur le zéro, c'est celle que j'essaierai en premier.
En 2012, un chercheur compilé une liste des codes PIN PIN les plus populaires à partir d'un certain nombre de violations de données. Ce qu'il a découvert, c'est que les PIN les plus populaires étaient soit:
- Séquences, telles que
1234ou7777 - Dates, comme
2001 - Références à la culture pop, telles que
0007(d'après le code 007 de James Bond) - Facile à taper, comme
2580(nombres qui se trouvent en ligne droite sur de nombreux claviers)
Voici le top 20 (qui n'inclut pas tous les exemples donnés ci-dessus): 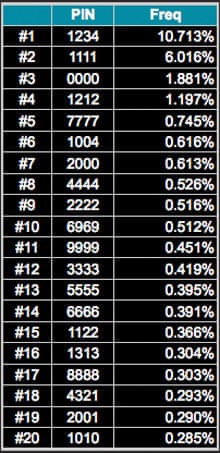
Donc, les séquences sont mauvaises. Il en va de même pour les codes PIN facilement mémorisables sans mnémonique. Cependant, les broches qui ont le même chiffre plusieurs fois ne sont pas nécessairement mauvaises également.
Exemple concret:
À l'autre extrémité de l'échelle, le nombre le moins utilisé que j'ai trouvé dans mon jeu de données était 8068. De toutes les combinaisons de nombres, cela semblait être le moins intéressant. Ce n'est pas une date dans l'histoire, ce n'est pas un modèle, ce n'est pas un anniversaire, ce n'est pas facile à taper. C'est l'épingle parfaite… ou ça l'aurait été jusqu'à présent.
Alors maintenant tu sais.
Sur mon téléphone, le PIN utilise délibérément l'un des nombres deux fois de suite, afin de le rendre plus difficile à deviner car:
- La quantité de "taches de graisse" ne correspond pas au nombre de chiffres
- Un "surfeur d'épaule" aura (un peu) plus de mal à distinguer le double tapotement du simple tapotement
Addendum: Le téléphone en question permet une longueur personnalisée du code PIN, donc un attaquant (ne respectant pas l'entrée de la broche) ne sait pas le nombre de chiffres dans utilisation.
Vous devriez faire une liste spécifique de "touches faibles" à l'avance, c'est ce que quelqu'un essaierait de deviner. Cela inclut des dates importantes, des adresses, etc. et peut inclure 1111 si les gens le font essayez cela lors de la supposition.
Faites ensuite un tirage au sort et filtrez par rapport à la (courte) liste. Si la liste n'est pas courte mais systématique (par exemple, pas de chiffres répétés, pas de dates légales), vous vous retrouvez avec trop peu de possibilités, ce qui facilite la devinette.
Il peut y avoir des attaques dont l'efficacité varie, selon le nombre de chiffres répétés.
Par exemple, supposons que quelqu'un applique une légère poussière sur le clavier de votre guichet. Vous insérez votre carte, vous couvrez les mains pendant que vous tapez votre épingle, vérifiez votre solde, puis vous étonnez. Au fur et à mesure, quelqu'un prend votre poche, récupère votre carte.
Ils ont maintenant votre carte et peuvent voir quels boutons ont leur époussetage perturbé - ils connaissent les chiffres, mais pas l'ordre.
S'ils voient que vous avez appuyé sur les chiffres 2, 3, 6 et 8, votre code PIN pourrait être l'un des suivants:
2368, 2386, 2638, 2683, 2836, 2863,
3268, 3286, 3628, 3682, 3826, 3862,
6238, 6283, 6328, 6382, 6823, 6832,
8236, 8263, 8326, 8362, 8623, 8632
24 possibilités. Avec 3 suppositions, ils ont 1/8 de chance de deviner correctement.
Voici les possibilités à 4 chiffres, dont l'un est répété: 2, 3 et 6:
2236, 2263, 2326, 2336, 2362, 2363,
2366, 2623, 2632, 2633, 2636, 2663,
3226, 3236, 3262, 3263, 3266, 3326,
3362, 3622, 3623, 3626, 3632, 3662,
6223, 6232, 6233, 6236, 6263, 6322,
6323, 6326, 6332, 6362, 6623, 6632
Il y en a 36. Les chances de deviner cela en 3 tentatives sont de 1/12. De meilleures chances!
Essayons à nouveau, cette fois avec seulement deux chiffres:
2223, 2232, 2233, 2322, 2323, 2332, 2333,
3222, 3223, 3232, 3233, 3322, 3323, 3332
14 combinaisons, plus de 1/5 chance de deviner avec 3 essais.
Évidemment, avec un seul chiffre, il n'y a qu'une seule solution, et on peut la deviner tout de suite.
Bien sûr, si les chiffres de votre épingle sont 1, 6 et 9, je suppose que vous êtes né en 1961, 1966, 1969 ou 1996 - si je vous vois partir, je devrais pouvoir deviner si vous avez 21 ou 48 ans, ce qui signifie que 3 suppositions sont probablement tout ce dont j'ai besoin.
Vous avez raison de dire que les règles de suppression des motifs nuiraient à votre espace clé, mais cela ne réduit pas l'entropie, car l'entropie provient de votre matériel, votre machine TRNG est autorisée à produire de temps en temps un chiffre répétitif.
Sur le calcul, si vous ne voulez pas voir un chiffre répétitif comme 9 dans '0919', alors votre calcul est correct, mais si vous voulez dire un chiffre répétitif comme 9 dans '0991', alors vous vous retrouvez avec 7190 sur 10000.
Mais en fonction de ce que vous pensez avec "quatre chiffres contenant une propriété ou un motif", vous le réduisez davantage, supprimez tous les motifs comme '12', 321 'ou' 34 ', supprimez tous les non premiers, alors vous n'en avez qu'une poignée ( ~ 300 sur 10000) de numéros sans intérêt.