Puzzle coulissant 5x5 Solution rapide et à faible mouvement
J'essaie de trouver un moyen de résoudre par programme un puzzle coulissant de 24 pièces dans un temps et des mouvements raisonnables. Voici un exemple de l'état résolu dans le puzzle que je décris:
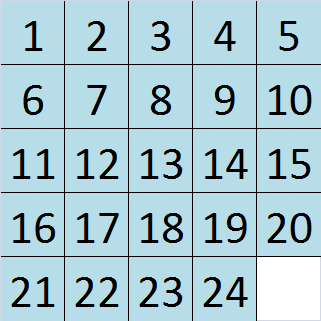
J'ai déjà trouvé que l'algorithme IDA * fonctionne assez bien pour accomplir cela pour un puzzle de 15 (grille 4x4). L'algorithme IDA * est capable de trouver le plus petit nombre de coups pour tout puzzle glissant 4x4 dans un laps de temps très raisonnable. J'ai exécuté une adaptation de this code pour tester des puzzles coulissants 4x4 et j'ai pu réduire considérablement le temps d'exécution en utilisant PyPy. Malheureusement, lorsque ce code est adapté aux énigmes coulissantes 5x5, il fonctionne horriblement lentement. Je l'ai couru pendant plus d'une heure et j'ai finalement renoncé à le voir finir, alors qu'il n'a fonctionné que quelques secondes sur des grilles 4x4. Je comprends que cela est dû au fait que le nombre de nœuds à rechercher augmente de manière exponentielle à mesure que la grille augmente. Cependant, je ne cherche pas à trouver la solution optimale à un puzzle coulissant 5x5, seulement une solution proche de l'optimum. Par exemple, si la solution optimale pour un puzzle donné était de 120 coups, alors je serais satisfait de toute solution inférieure à 150 coups et pouvant être trouvée en quelques minutes.
Y a-t-il des algorithmes spécifiques qui pourraient accomplir cela?
Un changement à deux caractères qui pourrait faire l'affaire est de multiplier l'heuristique par 2 (ou une autre constante). Ce n'est plus admissible, mais la solution trouvée sera dans un facteur de 2 optimal. Cette astuce s'appelle Weighted A */Static Weighting .